题目内容
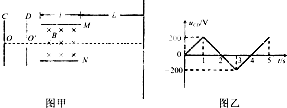 如图所示,C、D为平行正对的两金属板,在D板右方一边长为l=6.0cm的正方形区域内存在匀强磁场,该区域恰好在一对平行且正对的金属板M、N之间,M、N两板均接地,距板的右端L=12.0cm处放置一观察屏.在C、D两板间加上如图乙所示的交变电压,并从C板O处以每秒1 000个的频率均匀的源源不断地释放出电子,所有电子的初动能均为Ek0=120eV,初速度方向均沿OO′直线,通过电场的电子从M、N的正中间垂直射入磁场.已知电子的质量为m=9.0×10-31 kg,磁感应强度为B=6.0×10-4 T.问:
如图所示,C、D为平行正对的两金属板,在D板右方一边长为l=6.0cm的正方形区域内存在匀强磁场,该区域恰好在一对平行且正对的金属板M、N之间,M、N两板均接地,距板的右端L=12.0cm处放置一观察屏.在C、D两板间加上如图乙所示的交变电压,并从C板O处以每秒1 000个的频率均匀的源源不断地释放出电子,所有电子的初动能均为Ek0=120eV,初速度方向均沿OO′直线,通过电场的电子从M、N的正中间垂直射入磁场.已知电子的质量为m=9.0×10-31 kg,磁感应强度为B=6.0×10-4 T.问:(1)电子从D板上小孔O′点射出时,速度的最大值是多大?
(2)电子到达观察屏(观察屏足够大) 上的范围有多大?
(3)在uCD变化的一个周期内,有多少个电子能到达观察屏?
分析:(1)电子在CD间运动时,电场力做正功,动能增大,当UCD=200 V时,粒子获得最大速度,根据动能定理求解;
(2)电子进入磁场中做匀速圆周运动,洛伦兹力提供其向心力.速度最大时,轨迹半径;速度最小时,轨迹半径也最小.根据半径公式r=
求出电子轨迹的最大半径,画出轨迹示意图,由几何知识求出电子轨迹的最小半径,即可求得电子到达观察屏(观察屏足够大) 上的范围.
(3)先根据轨迹半径公式求出半径最小时,由动能定理求出CD间的电压UCD1.则在uCD变化的一个周期内,即可时间与周期的关系求解.
(2)电子进入磁场中做匀速圆周运动,洛伦兹力提供其向心力.速度最大时,轨迹半径;速度最小时,轨迹半径也最小.根据半径公式r=
| mv |
| qB |
(3)先根据轨迹半径公式求出半径最小时,由动能定理求出CD间的电压UCD1.则在uCD变化的一个周期内,即可时间与周期的关系求解.
解答: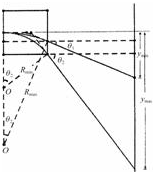 解:(1))当UCD=200 V时,电子获得最大速度vmax.由动能定理得:eUCD=
解:(1))当UCD=200 V时,电子获得最大速度vmax.由动能定理得:eUCD=
m
-
m
得最大速度vmax=
×106 m/s;
(2)电子在磁场中的最大半径:Rmax=
=10 cm
设电子在磁场中最大的偏转角为θ1,则有
sinθ1=
=
在荧光屏上最小的偏转距离为:
ymin=Rmax(1-cosθ1)+Ltanθ1=11 cm.
最小半径应满足:
=l2+(Rmin-
)2
∴Rmin=7.5 cm,sinθ2=
=
在荧光屏上最在的偏转距离为:
ymax=
+Ltanθ2=19 cm
∴电子到达观察屏(观察屏足够大) 上的范围为:△y=ymax-ymin=8 cm.
(3)电子的最小半径为:Rmin=
设对应的加速电压为UCD1.
根据动能定理得:eUCD1=
m
-Ek0;
∴UAB1=60 V
∴n=2
×1000=2×
×1000=1400(个)
答:
(1)电子从D板上小孔O′点射出时,速度的最大值是
×106 m/s;
(2)电子到达观察屏(观察屏足够大) 上的范围有8cm.
(3)在uCD变化的一个周期内,有1400个电子能到达观察屏.
 解:(1))当UCD=200 V时,电子获得最大速度vmax.由动能定理得:eUCD=
解:(1))当UCD=200 V时,电子获得最大速度vmax.由动能定理得:eUCD=| 1 |
| 2 |
| v | 2 max |
| 1 |
| 2 |
| v | 2 0 |
得最大速度vmax=
| 32 |
| 3 |
(2)电子在磁场中的最大半径:Rmax=
| mvmax |
| eB |
设电子在磁场中最大的偏转角为θ1,则有
sinθ1=
| l |
| Rmax |
| 3 |
| 5 |
在荧光屏上最小的偏转距离为:
ymin=Rmax(1-cosθ1)+Ltanθ1=11 cm.
最小半径应满足:
| R | 2 min |
| 1 |
| 2 |
∴Rmin=7.5 cm,sinθ2=
| 1 |
| Rmin |
| 4 |
| 5 |
在荧光屏上最在的偏转距离为:
ymax=
| l |
| 2 |
∴电子到达观察屏(观察屏足够大) 上的范围为:△y=ymax-ymin=8 cm.
(3)电子的最小半径为:Rmin=
| mvmin |
| eB |
设对应的加速电压为UCD1.
根据动能定理得:eUCD1=
| 1 |
| 2 |
| v | 2 min |
∴UAB1=60 V
∴n=2
| Um-UCD1 |
| Um |
| 200-60 |
| 200 |
答:
(1)电子从D板上小孔O′点射出时,速度的最大值是
| 32 |
| 3 |
(2)电子到达观察屏(观察屏足够大) 上的范围有8cm.
(3)在uCD变化的一个周期内,有1400个电子能到达观察屏.
点评:本题中根据动能定理求电子加速得到的速度,在磁场中,画出电子的运动轨迹,运用几何知识进行分析和计算相关的距离,都是常用的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图所示,A、B为平行板电容器的金属板,C为静电计,开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大些,应该采取的措施是( )
如图所示,A、B为平行板电容器的金属板,C为静电计,开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大些,应该采取的措施是( )| A、断开开关S后,将A、B两极板靠近些 | B、断开开关S后,将A、B两极板分开些 | C、保持开关S闭合,将A、B两极板靠近些 | D、保持开关S闭合,将变阻器滑动触头向上移动 |
 如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( )
如图所示,A、B为平行板电容器的金属板,G为静电计,开始时开关S闭合,静电计指针张开一定角度.下述结论正确的是( ) (2011?重庆模拟)如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大一些,应该采取的措施是( )
(2011?重庆模拟)如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计指针张开一定角度.为了使指针张开角度增大一些,应该采取的措施是( ) 如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计的指针张开了一定的角度.为了使指针张开的角度变小,可以采取的一项措施是:
如图所示,A、B为平行板电容器的金属板,G为静电计.开始时开关S闭合,静电计的指针张开了一定的角度.为了使指针张开的角度变小,可以采取的一项措施是: