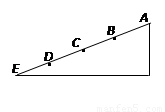题目内容
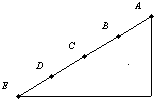 如图,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体由A点由静止释放,下列结论正确的是( )
如图,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体由A点由静止释放,下列结论正确的是( )分析:A、根据v2=2ax,可求出物体到达各点的速度之比.
B、初速度为零的匀加速运动的推论:tB:tC:tD:tE=1:
:
:2.根据这个结论判断时间关系.
C、AB段和BE段的位移比为1:3,可知两段位移所用的时间相等,某段时间内的平均速度等于中间时刻的瞬时速度.
D、看每一段位移所用的时间是否相同去判断速度的增量关系.
B、初速度为零的匀加速运动的推论:tB:tC:tD:tE=1:
| 2 |
| 3 |
C、AB段和BE段的位移比为1:3,可知两段位移所用的时间相等,某段时间内的平均速度等于中间时刻的瞬时速度.
D、看每一段位移所用的时间是否相同去判断速度的增量关系.
解答:解:A、根据v2=2ax,v=
,知物体到达各点的速度vB:vC:vD:vE=1:
:
:2.故A正确,
B、因为v=at,所以有tB:tC:tD:tE=vB:vC:vD:vE=1:
:
:2,所以tE=2tB=
tC=
tD.故B正确.
C、AB段和BE段的位移比为1:3,可知两段位移所用的时间相等,某段时间内的平均速度等于中间时刻的瞬时速度.所用物体从A运动到E的全过程平均速度
=vB.故C错误.
D、物体通过每一部分时间不等,所以速度的增量不等.故D错误.
故选AB.
| 2ax |
| 2 |
| 3 |
B、因为v=at,所以有tB:tC:tD:tE=vB:vC:vD:vE=1:
| 2 |
| 3 |
| 2 |
| 2 | ||
|
C、AB段和BE段的位移比为1:3,可知两段位移所用的时间相等,某段时间内的平均速度等于中间时刻的瞬时速度.所用物体从A运动到E的全过程平均速度
. |
| v |
D、物体通过每一部分时间不等,所以速度的增量不等.故D错误.
故选AB.
点评:解决本题的关键掌握速度位移公式v2-v02=2ax,以及知道某段时间内的平均速度等于中间时刻的瞬时速度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
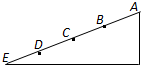 如图,光滑斜面AE被分成四个相等的部分,一个物体由A点静止释放,下面结论中正确的是( )
如图,光滑斜面AE被分成四个相等的部分,一个物体由A点静止释放,下面结论中正确的是( )A、物体到达各点的速度vB:vC:vD::vE=1:
| ||||
B、物体到达各点所经历的时间tB:tC:tD::tE=1:
| ||||
| C、物体从A到E的平均速度v=vB | ||||
| D、经过每一部分时,其速度增量均相同 |
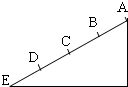 如图,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论正确的是( )
如图,光滑斜面AE被分成四个相等的部分,一物体由A点从静止释放,下列结论正确的是( )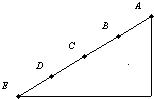 如图,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体由A点由静止释放,下列结论正确的是( )
如图,光滑斜面AE被分成四个长度相等的部分,即AB=BC=CD=DE,一物体由A点由静止释放,下列结论正确的是( )