题目内容
【题目】如图,赤道上空有2颗人造卫星A、B绕地球做同方向的匀速圆周运动,地球半径为R,卫星A为近地卫星,卫星B的轨道半径为2R,卫星B的运动周期为T,某时刻2颗卫星与地心在同一直线上,则
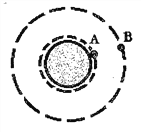
A. 卫星A的加速度小于B的加速度
B. 卫星A、B的周期之比为1: ![]()
C. 在地球表面上发射卫星B的速度要小于第二宇宙速度
D. 若万有引力常量G已知,根据题中数据可以求出地球的平均密度
【答案】BCD
【解析】A、卫星绕地球做匀速圆周运动,万有引力提供向心力有: ![]() ,则有加速度大小
,则有加速度大小![]() ,由于卫星A为近地卫星,卫星B的轨道半径为2R,所以卫星A的加速度大于卫星B的加速度,故A错误;
,由于卫星A为近地卫星,卫星B的轨道半径为2R,所以卫星A的加速度大于卫星B的加速度,故A错误;
B、万有引力提供向心力有: ![]() ,则有周期
,则有周期![]() ,卫星A、B的周期之比为
,卫星A、B的周期之比为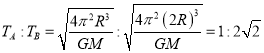 ,故B正确;
,故B正确;
C、物体在地面附近绕地球做匀速圆周运动的速度叫做第一宇宙速度,在地面附近发射卫星,速度大于7.9km/s,而小于11.2km/s,所以在地球表面上发射卫星B的速度要小于第二宇宙速度,故C正确;
D、对于卫星B,万有引力提供向心力有: 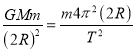 ,解得
,解得![]() ,地球的平均密度
,地球的平均密度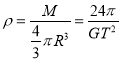 ,故D正确;
,故D正确;
故选BCD。

练习册系列答案
相关题目