题目内容
3.如图甲所示,质量M=1.0kg的长木板A静止在光滑水平面上,在木板的左端放置一个质量m=2.0kg的小铁块B,铁块与木板间的动摩擦因数μ=0.1,对铁块施加水平向右的拉力F,F大小随时间变化如图乙所示,4s时撤去拉力.可认为A、B间的最大静摩擦力与滑动摩擦力大小相等,取重力加速度g=10m/s2.求: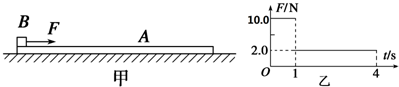
(1)0-1s内,A、B的加速度大小aA、aB;
(2)若要使小铁块B不会从长木板A上滑落,长木板至少多长;
(3)4s内摩擦力对小铁块B做的功.
分析 (1)分别对两物体受力分析,由牛顿第二定律可求得两物体的加速度;
(2)分析两物体的运动过程,求出速度相等的时间;则由位移公式求得两物体的位移,则位移之差为长木板的位移;
(3)先求出二者具有共同速度的位移,求出摩擦力做的功;再求出共同速度后二者之间的摩擦力及位移,再据功的定义式求摩擦力所做的功,再求4秒内功即可求解.
解答 解:(1)在0~1s内,A、B两物体分别做匀加速直线运动,根据牛顿第二定律可得:
μmg=MaA
F1-μmg=maB
代入数据得:aA=2m/s2;aB=4m/s2;
(2)当t1=1s后,拉力F2=μmg,铁块B做匀速运动,速度大小为v1,木板A仍做匀加速直线运动,又经过时间t2,速度与铁块B相等
v1=aBt1
又v1=aA(t1+t2)
解得:t2=1s;v1=4m/s
此过程中A的位移:sA=$\frac{{v}_{1}^{2}}{2{a}_{A}}$=$\frac{16}{2×2}m$=4m
B的位移为:sB=$\frac{1}{2}×4×1m$+4×1m=6m
所以长木板的长度:L=sB-sA=2m
(3)设A、B速度相等后一起做匀加速直线运动,运动时间t3=2s,共同的加速度为a,
F2=(M+m)a
解得:a=$\frac{2}{3}$m/s2
据牛顿第二定律得,二者之间的摩擦力为:f1=Ma=$\frac{2}{3}$N
2s到4s运动的位移为:s=4×2m+$\frac{1}{2}×\frac{2}{3}×{2}^{2}$m=$\frac{28}{3}m$
所以在2秒内摩擦力对铁块做的功:W1=-fsB=-12J
2s到4s内摩擦力做的功为:W2=-f1•s=-$\frac{56}{9}J$
所以4秒内摩擦力对铁块做的总功为:W=-$\frac{164}{9}$J
答:(1)0~ls内,A、B的加速度大小aA、aB;为2m/s2和4m/s2;(2)长木板的长度至少为2m;(3)0~4s内,摩擦力对小铁块B做的功-$\frac{164}{9}$J.
点评 本题综合考查牛顿第二定律、运动学公式及功的公式等内容,要注意做好正确的受力分析及过程分析,应用牛顿第二定律及运动学公式等求解.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案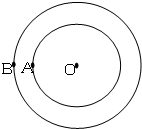 如图所示,A、B两质点绕同一圆心按顺时针方向做匀速圆周运动,A的周期为T1,B的周期为T2,且T1<T2,在某时刻两质点相距最近,开始计时,则以下选项中符合两质点相距最近的时间为(其中n=1、2、3…)( )
如图所示,A、B两质点绕同一圆心按顺时针方向做匀速圆周运动,A的周期为T1,B的周期为T2,且T1<T2,在某时刻两质点相距最近,开始计时,则以下选项中符合两质点相距最近的时间为(其中n=1、2、3…)( )| A. | $\frac{{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}}$ | B. | $\frac{n{T}_{1}{T}_{2}}{{T}_{2}-{T}_{1}}$ | C. | n(T2-T1) | D. | $\frac{{T}_{1}{T}_{2}}{2({T}_{2}-{T}_{1})}$ |
 图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )
图中实线表示某一平面内的电场线,虚线表示等势线,A、B是电场中的两点.以下说法中正确的是( )| A. | A点电势较高 | |
| B. | 电子在A点的电势能较大 | |
| C. | 将正电荷从B移动到A,静电力做负功 | |
| D. | A、B两点间的电势差UAB是正的 |
 如图所示,沿波的传播方向上有间距均为1m的a,b,c,d,e,f六个质点,都处在各自的平衡位置.一列波以1m/s的速度水平向右传播,t=0s时到达质点a,a开始由平衡位置向上运动,t=1s时,a第一次到达最高点,在4s<t<5s这段时间内下列说法错误的是( )
如图所示,沿波的传播方向上有间距均为1m的a,b,c,d,e,f六个质点,都处在各自的平衡位置.一列波以1m/s的速度水平向右传播,t=0s时到达质点a,a开始由平衡位置向上运动,t=1s时,a第一次到达最高点,在4s<t<5s这段时间内下列说法错误的是( )| A. | 质点d向下运动 | B. | 质点f保持静止 | ||
| C. | 质点c的加速度逐渐增大 | D. | 质点a的速度逐渐增大 |
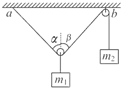 在如图所示装置中,两物体质量分别为m1、m2,悬点a、b间的距离远大于滑轮的直径,不计一切摩擦,整个装置处于静止状态.由图可知( )
在如图所示装置中,两物体质量分别为m1、m2,悬点a、b间的距离远大于滑轮的直径,不计一切摩擦,整个装置处于静止状态.由图可知( )| A. | m1可能大于2m2 | |
| B. | m1一定小于2m2 | |
| C. | α一定等于β | |
| D. | 当把悬点a向左缓慢移动时,绳子上的张力不会变 |
| A. | 通过闭合电路磁通量很大 | B. | 通过闭合电路磁通量很小 | ||
| C. | 通过闭合电路磁通量不变 | D. | 通过闭合电路磁通量改变 |


 如图所示,均匀金属电阻丝焊接成半径为a的圆环,总电阻为2R,匀强磁场磁感应强度为B,垂直穿过环所在平面.电阻为R的金属杆 AB沿环表面以速度v向右滑至环中央时,(1)杆两端的电压为?
如图所示,均匀金属电阻丝焊接成半径为a的圆环,总电阻为2R,匀强磁场磁感应强度为B,垂直穿过环所在平面.电阻为R的金属杆 AB沿环表面以速度v向右滑至环中央时,(1)杆两端的电压为?