题目内容
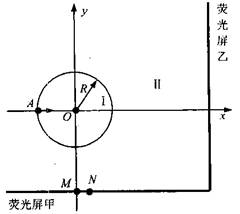
如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(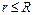 )和圆外区域Ⅱ(
)和圆外区域Ⅱ(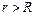 )分别存在两个磁场方向均垂直于
)分别存在两个磁场方向均垂直于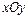 平面的匀强磁场;垂直于
平面的匀强磁场;垂直于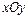 平面放置了两块平面荧光屏,其中荧光屏甲平行于
平面放置了两块平面荧光屏,其中荧光屏甲平行于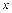 轴放置在
轴放置在 轴坐标为
轴坐标为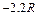 的位置,荧光屏乙平行于
的位置,荧光屏乙平行于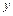 轴放置在
轴放置在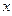 轴坐标为
轴坐标为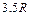 的位置。现有一束质量为
的位置。现有一束质量为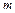 、电荷量为
、电荷量为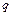 (
(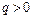 )、动能为
)、动能为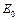 的粒子从坐标为(
的粒子从坐标为(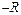 ,0)的
,0)的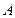 点沿
点沿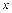 轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现坐标为(
轴正方向射入区域Ⅰ,最终打在荧光屏甲上,出现坐标为(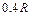 ,
,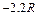 )的亮点
)的亮点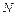 。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(
。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(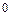 ,
,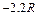 )的亮点
)的亮点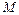 。此时,若将荧光屏甲沿
。此时,若将荧光屏甲沿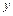 轴负方向平移,则亮点的
轴负方向平移,则亮点的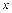 轴坐标始终保持不变。(不计粒子重力影响)
轴坐标始终保持不变。(不计粒子重力影响)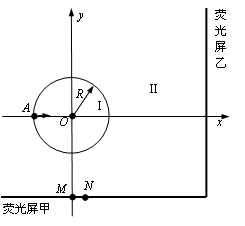
(1)求在区域Ⅰ和Ⅱ中粒子运动速度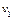 、
、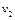 的大小。
的大小。
(2)求在区域Ⅰ和Ⅱ中磁感应强度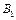 、
、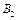 的大小和方向。
的大小和方向。
(3)若上述两个磁场保持不变,荧光屏仍在初始位置,但从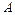 点沿
点沿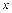 轴正方向射入区域Ⅰ的粒子束改为质量为
轴正方向射入区域Ⅰ的粒子束改为质量为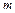 、电荷量为
、电荷量为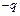 、动能为
、动能为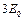 的粒子,求荧光屏上的亮点的位置。
的粒子,求荧光屏上的亮点的位置。
(1)由于在磁场中运动时洛仑兹力不做功,所以在区域Ⅰ和Ⅱ中粒子运动速度大小就是在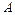 点入射时初始速度大小
点入射时初始速度大小 ,由
,由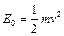 可得
可得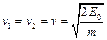 ① (2分)
① (2分)
(1)粒子在区域Ⅰ中运动了四分之一圆周后,从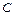 点沿
点沿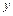 轴负方向进入区域Ⅱ的磁场。如图所示,圆周运动的圆心是
轴负方向进入区域Ⅱ的磁场。如图所示,圆周运动的圆心是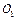 点,半径为
点,半径为
(2)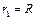 ② (2分)
② (2分)
由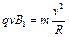 可得
可得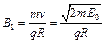
 ③ (2分)
③ (2分)
方向垂直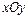 平面向外。 ④ (1分)
平面向外。 ④ (1分)
粒子进入区域Ⅱ后做半径为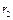 的圆周运动,由
的圆周运动,由
可得 ⑤
⑤
圆 周运动的圆心
周运动的圆心 坐标为(
坐标为(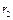 ,
,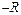 ),圆周运动轨迹方程为
),圆周运动轨迹方程为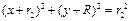
将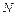 点的坐标(
点的坐标(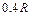 ,
,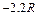 )代入上式,可得
)代入上式,可得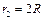 ⑥ (2分)
⑥ (2分)
利用⑤、⑥式得 ⑦ (2分)
⑦ (2分)
方向垂直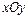 平面向里。
平面向里。  ⑧ (1分)
⑧ (1分)
(3)如图所示,粒子先在区域Ⅰ中做圆周运动。由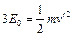 可知,运动速度为
可知,运动速度为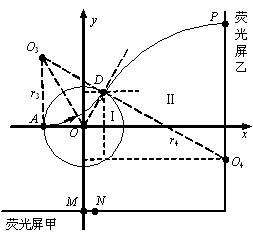
 类似于⑤式,半径为
类似于⑤式,半径为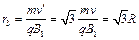 ⑨ (2分)
⑨ (2分)
由圆心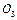 的坐标(
的坐标(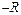 ,
,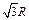 )可知,
)可知, 与
与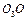 的夹角为
的夹角为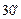 。通过分析如图的几何关系,粒子从
。通过分析如图的几何关系,粒子从 点穿出区域Ⅰ的速度方向与
点穿出区域Ⅰ的速度方向与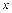 轴正方向的夹角为
轴正方向的夹角为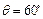 ⑩ (3分)
⑩ (3分)
粒子进入区域Ⅱ后做圆周运动的半径为 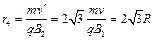 (2分)
(2分)
其圆心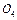 的坐标为(
的坐标为(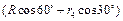 ,
,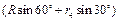 ),即(
),即( ,
,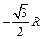 ),说明圆心
),说明圆心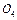 恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的
恰好在荧光屏乙上。所以,亮点将出现在荧光屏乙上的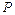 点,其
点,其 轴坐标为
轴坐标为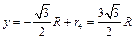 (3分
(3分
解析

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 (2011?石景山区一模)如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(r≤R)和圆外区域Ⅱ(r>R)分别存在两个匀强磁场,方向均垂直于xOy平面.垂直于xOy平面放置两块平面荧光屏,其中荧光屏甲平行于x轴放置在
(2011?石景山区一模)如图所示,圆心在原点、半径为R的圆将xOy平面分为两个区域,在圆内区域Ⅰ(r≤R)和圆外区域Ⅱ(r>R)分别存在两个匀强磁场,方向均垂直于xOy平面.垂直于xOy平面放置两块平面荧光屏,其中荧光屏甲平行于x轴放置在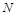 。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)
。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(0,-2.2R)的亮点M。此时,若将荧光屏甲沿Y轴负方向平移,则亮点的X轴坐标始终保持不变。(不计粒子重力影响)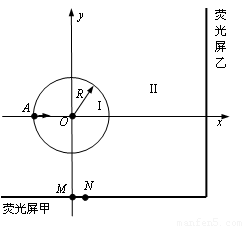
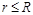 )和圆外区域Ⅱ(
)和圆外区域Ⅱ(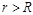 )分别存在两个磁场方向均垂直于
)分别存在两个磁场方向均垂直于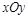 平面的匀强磁场;垂直于
平面的匀强磁场;垂直于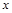 轴放置在
轴放置在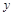 轴坐标为
轴坐标为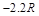 的位置,荧光屏乙平行于
的位置,荧光屏乙平行于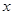 轴坐标为
轴坐标为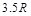 的位置。现有一束质量为
的位置。现有一束质量为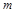 、电荷量为
、电荷量为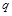 (
(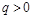 )、动能为
)、动能为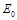 的粒子从坐标为(
的粒子从坐标为(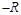 ,0)的
,0)的 点沿
点沿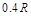 ,
,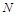 。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(
。若撤去圆外磁场,粒子打在荧光屏甲上,出现坐标为(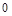 ,
,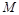 。此时,若将荧光屏甲沿
。此时,若将荧光屏甲沿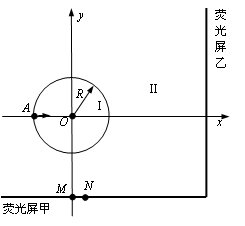
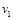 、
、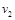 的大小。
的大小。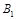 、
、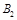 的大小和方向。
的大小和方向。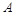 点沿
点沿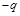 、动能为
、动能为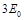 的粒子,求荧光屏上的亮点的位置。
的粒子,求荧光屏上的亮点的位置。