题目内容
【题目】如图所示，在直角坐标系xOy的第一象限中两个相同的直角三角形区域Ⅰ、Ⅱ内分别充满了方向相反、磁感应强度大小均为B的匀强磁场，已知C点坐标为(
，l)，质量为m，带电荷量为q的正电荷从A(
，l)点以一定的速度平行于y方向垂直进入磁场，并从x轴上的D点(图中未画出)垂直x轴离开磁场，电荷重力不计。
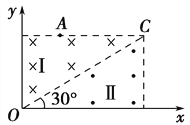
(1)求D点的位置坐标及电荷进入磁场区域Ⅰ时的速度大小v；
(2)若将区域Ⅱ内的磁场换成沿－x轴方向的匀强电场，该粒子仍从A点以原速度进入磁场区域Ⅰ，并最终仍能垂直x轴离开，求匀强电场的场强E。
【答案】(1)
(2)
【解析】
(1)根据粒子运动的对称性可知，粒子从OC的中点O′进入磁场区域Ⅱ，且AC＝OD，则D的坐标为(
l，0)。设粒子在磁场中运动的半径为r，在磁场Ⅰ中的轨迹所对圆心角为θ，
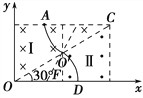
根据几何知识可知rsin θ＝
l，
r－rcos θ＝
l－
l，
解得θ＝
，r＝l。
粒子在磁场中做圆周运动，qvB＝m
，
速度大小
，
故
(2)设粒子在电场中的运动时间为t，加速度大小为a，
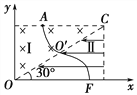
则根据运动的分解可知，在x轴方向：0－vsin θ＝－at，
在y轴方向：vtcos θ＝l，其中，qE＝ma，
联立解得:
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
