题目内容
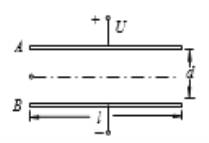
【题目】一水平放置的平行板电容器,两极板间距为d,极板分别与理想电源两极相连(极板间电场可视为匀强电场)。上极板中心有一小孔(小孔对电场的影响可忽略不计).一质量为m电荷量为+q的小球从小孔正上方![]() 处由静止开始下落(不计空气阻力,重力加速度为g),经过小孔进入电容器,到达下极板处速度恰好为零并返回(未与下极板接触).求:
处由静止开始下落(不计空气阻力,重力加速度为g),经过小孔进入电容器,到达下极板处速度恰好为零并返回(未与下极板接触).求:
(1)小球到达小孔处的速度;
(2)极板间电场强度大小;
(3)若将下极板向上平移d/4,则同样下落的小球将在距上极板多远处返回.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
下极板未移动时,带电粒子到达下极板处返回,知道重力做功与电场力做功之和为零,向上移动下极板,若运动到下极板,重力做功小于克服电场力做功,可知不可能运动到下极板返回,依据动能定理求解.
(1)设小球到达上级板的速度为v,此过程运用动能定理得:![]()
解得:![]()
(2)对小球由全过程的动能定理:![]()
解得:![]()
(3)设小球在距上极板h处速度减为零,
因电容器与理想电源一直连接,则电容器的电压U不变,则场强![]()
下极板上移![]() 后,场强为
后,场强为![]()
即![]()
在小球重庆下落过程,由动能定理:![]()
解得:![]()

练习册系列答案
相关题目