题目内容
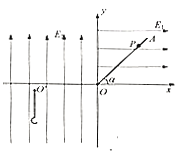
【题目】如图所示，在竖直平面内的xOy直角坐标系中，第1象限内分布着沿x轴正方向的匀强电场
，第Ⅱ象限和第Ⅲ象限分布着沿y轴正方向的匀强电场
在第I象限内有一与x轴正方向成
角的固定光滑绝缘杆AO，第Ⅲ象限有一用轻绳悬挂于
点的弧形轻质筐。现有一可看成质点、套在杆AO上的带电小球P以速度
沿杆匀速下滑，小球从坐标原点O离开后进入第Ⅲ象限，运动一段时间恰好沿水平方向进入弧形轻质筐内，在小球进入弧筐的同时将匀强电场
的大小不变，方向改为沿x轴正方向，随后小球恰能在坐标系中做完整的圆周运动。已知小球的质量为
，电荷量
，第Ⅱ象限和第Ⅲ象限的场强
，悬点O的横坐标
。弧筐的重量忽略不计，大小远小于轻绳长度，重力加速度为
求：
小球的电性及第1象限内电场的电场强度；
小球在绝缘杆AO上匀速运动的速度；
悬挂弧筐的轻绳的长度L。
【答案】
；
；
。
【解析】
带电小球P以速度
沿杆匀速下滑，根据平衡可求得小球的电性及第1象限内电场的电场强度
；小球进入第Ⅲ象限后受电场力和重力做斜抛运动，在x方向做匀速直线运动，y方向做匀变速直线运动，根据两方向运动规律列式求解；小球恰能在坐标系中做完整的圆周运动，在等效最高点只有重力和电场力的提供向心力求出最高点的速度，再根据动能定理列式求解即可。
小球再沿杆做匀速运动时，由受力分析可知小球带正电，且又：
解得：
小球进入第Ⅲ象限后受到电场力和重力做斜抛运动，在x方向做匀速直线运动，在y方向做匀变速直线运动，由题意可知：
x：
y：
联立解得：
小球进入弧筐后做圆周运动，设等效最高点小球受到的电场力和重力的合力大小为F，此时电场力与水平方向夹角为
，则
设小球到达等效最高点B的速度为v，因恰能做完整的圆周运动，
由牛顿第二定律得：
设绳长为L，小球进入弧筐后到达B的过程中，由动能定理得：
联立解得：
