��Ŀ����
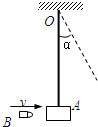 ��ͼ��ʾ��Сľ��A��ϸ�ߵ���O�㣬�˿�С������������Ϊ�㣮һ���ӵ���һ����ˮƽ�ٶ�����ľ��A�У���������A�й�ͬ���ٶȣ�Ȼ��һ��ڶ������ڽǦ�����������ӵ�������������ٶȴ�С���䣬��ʹСľ������������������ڽǦ����ӵ��ij�������ľ����ӵ�һ��ﵽ���ڽ�ʱ�Ļ�е��֮���E���У�������
��ͼ��ʾ��Сľ��A��ϸ�ߵ���O�㣬�˿�С������������Ϊ�㣮һ���ӵ���һ����ˮƽ�ٶ�����ľ��A�У���������A�й�ͬ���ٶȣ�Ȼ��һ��ڶ������ڽǦ�����������ӵ�������������ٶȴ�С���䣬��ʹСľ������������������ڽǦ����ӵ��ij�������ľ����ӵ�һ��ﵽ���ڽ�ʱ�Ļ�е��֮���E���У��������������ӵ�����ľ��Ĺ����ж����غ㣬��ľ�����ӵ��ڶ��Ĺ����У���е���غ㣬�����ӵ��ij�������ľ����ӵ�һ��ﵽ���ڽ�ʱ�Ļ�е��֮���E�����ӵ�����ľ������л�е�ܵ���ʧ��
����⣺���ݶ����غ�ã�mv=��M+m��v�䣬���v��=
��
С������ӵ�ϵͳ�Ļ�е��E2=
(M+m)v��2=
��Сľ�������M������ϵͳ��е�ܼ�С���ﵽ���İڽǼ�С��
ϵͳ��е�ܵ���ʧ��E=
mv2-E2=
mv2(1-
)��M�������E����C��ȷ��A��B��D����
��ѡC��
| mv |
| M+m |
С������ӵ�ϵͳ�Ļ�е��E2=
| 1 |
| 2 |
| mv2 |
| 2(M+m) |
ϵͳ��е�ܵ���ʧ��E=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| M+m |
��ѡC��
�����������ۺϿ����˶����غ㶨�ɡ���е���غ㶨���Լ������غ㶨�ɣ�֪���ӵ��ij�������ľ����ӵ�һ��ﵽ���ڽ�ʱ�Ļ�е��֮���E�����ӵ�����ľ������л�е�ܵ���ʧ��

��ϰ��ϵ�д�
 ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ
 ��2011?˫����ģ�⣩��ͼ��ʾ��Сľ��A��ϸ�ߵ���O�㣬�˿�С������������Ϊ�㣮һ���ӵ���һ����ˮƽ�ٶ�����ľ��A�У���������A�й�ͬ���ٶȣ�Ȼ��һ��ڶ������ڽǦ�������900�������ƿ�����������������ӵ������ٶȴ�С���䣬��ʹ�ӵ�����������������һ��ڶ������ڽ� �����ӵ���A��ɵ�ϵͳ��ʧ�Ļ�е�ܡ�E���У�������
��2011?˫����ģ�⣩��ͼ��ʾ��Сľ��A��ϸ�ߵ���O�㣬�˿�С������������Ϊ�㣮һ���ӵ���һ����ˮƽ�ٶ�����ľ��A�У���������A�й�ͬ���ٶȣ�Ȼ��һ��ڶ������ڽǦ�������900�������ƿ�����������������ӵ������ٶȴ�С���䣬��ʹ�ӵ�����������������һ��ڶ������ڽ� �����ӵ���A��ɵ�ϵͳ��ʧ�Ļ�е�ܡ�E���У�������
