Question

【题目】如图所示，质量为mB=2kg的平板车B上表面水平，开始时静止在光滑水平面上，在平板车左端静止着一块质量为mA=2kg的物体A，一颗质量为m0=0.01kg的子弹以v0=600m/s的水平初速度瞬间射穿A后，速度变为v2=200m/s，已知A、B之间的动摩擦因数为μ=0.25，g取10m/s2，为使物块A不滑离小车B，则：

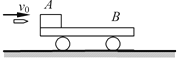
（1）小车的长度至少为多少？

（2）物块A与小车B发生相对滑动的时间多长？

Answer 1

【答案】(1) 0.4m (2) 0.4s

【解析】（1）对于子弹与物块A相互作用的过程，由动量守恒定律得：
m0v0=m0v+mAmA
代入数据解得：vA=2m/s
对于A、B相互作用的过程，由动量守恒定律得：
mAvA=（mA+mB）vB
代入数据解得：vB=1m/s
A、B系统因摩擦产生的热量等于A、B系统损失的动能，设小车的最短长度l，有：
μmAgl＝mAvA2(mA+mB)vB2
代入数据解得：l=0.4m
（2）对小车B，根据动量定理，有：μmAgt＝mBvB
代入数据解得：t=0.4s