Question

（13）质量为m＝0.02 kg的通电细杆AB置于倾角为θ＝37°的平行放置的导轨上，导轨的宽度L＝0.2 m，杆AB与导轨间的动摩擦因数μ＝0.4，磁感应强度B＝2 T的匀强磁场与导轨平面垂直且方向向下，如图所示．电池内阻不计，电阻R＝16Ω，AB棒电阻r =4Ω试求出为使杆AB静止不动，电池电动势的范围应是多少？（sin37°=0.6  cos37°=0.8）

 

 

Answer 1

【答案】

电池电动势的范围应是2.8V-9.2V

【解析】

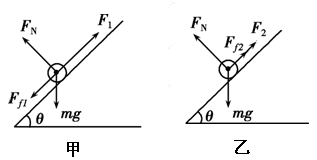
试题分析：杆AB中的电流为从A到B，所受的安培力方向平行于导轨向上.当电流较大时，导体有向上的运动趋势，所受静摩擦力向下;当静摩擦力达到最大时，磁场力为最大值F₁，此时通过AB的电流最大为I_max；电池电动势最大E_max，同理，当电流最小时，应该是导体受向上的最大静摩擦力，此时的安培力为F₂，电流为I_min. 电池电动势最小E_min。正确地画出两种情况下的受力图如图甲、乙，由平衡条件列方程求解。

根据甲受力图列式如下：由物体的平衡

 F₁-mgsinθ-F_f1=0  ，F_N-mgcosθ=0  F_f1=μF_N  ，F₁=BI_maxd，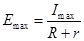

解上述方程得：E_max=9.2V

 根据乙受力图由物体的平衡：

F₂+F_f2-mgsinθ=0，F_N-mgcosθ=0，F_f2=μF_N  ，F₂=BI_mind，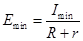

 解上述方程得：E_min=2.8V

电池电动势的范围应是2.8V-9.2V

考点：物体的平衡 左手定则 安培力 闭合电路欧姆定律