题目内容
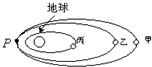 地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示的三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切.不计阻力,以下说法正确的是( )
地球赤道上的重力加速度为g,物体在赤道上随地球自转的向心加速度为a,卫星甲、乙、丙在如图所示的三个椭圆轨道上绕地球运行,卫星甲和乙的运行轨道在P点相切.不计阻力,以下说法正确的是( )分析:根据发射速度大小,分析卫星发射的难易程度,发射速度越大,发射越困难.机械能跟卫星的速度、高度和质量有关,质量未知时,是无法比较卫星的机械能大小的.根据开普勒第三定律知,椭圆半长轴越大,卫星的周期越大.由牛顿第二定律研究加速度.
解答:解:A、使地球上的物体票“飘”起来即物体处于完全失重状态,即此时物体所受地球的重力完全提供物体随地球自转时的向心力则有:
G
-mg=ma
当物体飘起来的时候,万有引力完全提供向心力,则此时物体的向心加速度为
=m(g+a)即此时的向心加速度a′=g+a
根据向心加速度和转速的关系有:a=R(n2π)2,a′=R(n′2π)2可得:n′=
n=
n
故A正确.
B、物体在椭圆形轨道上运动,轨道高度超高,在近地点时的速度越大,故B错误;
C、根据开普勒第三定律知,椭圆半长轴越小,卫星的周期越小,卫星丙的半长轴最短,故周期最小.
D、卫星的机械能跟卫星的速度、高度和质量有关,因未知卫星的质量,故不能确定甲卫星的机械能最大,故D错误.令卫星做匀速圆周运动时,万有引力完全提供圆周运动的向心力,故此时卫星中宇航员处于完全失重状态,但当卫星沿椭圆轨道运动时,卫星所受万有引力不是完全提供卫星的向心力,故卫星中宇航员始终处于完全失重状态是错误的.
故选AC.
G
| mM |
| R2 |
当物体飘起来的时候,万有引力完全提供向心力,则此时物体的向心加速度为
| GmM |
| R2 |
根据向心加速度和转速的关系有:a=R(n2π)2,a′=R(n′2π)2可得:n′=
|
|
故A正确.
B、物体在椭圆形轨道上运动,轨道高度超高,在近地点时的速度越大,故B错误;
C、根据开普勒第三定律知,椭圆半长轴越小,卫星的周期越小,卫星丙的半长轴最短,故周期最小.
D、卫星的机械能跟卫星的速度、高度和质量有关,因未知卫星的质量,故不能确定甲卫星的机械能最大,故D错误.令卫星做匀速圆周运动时,万有引力完全提供圆周运动的向心力,故此时卫星中宇航员处于完全失重状态,但当卫星沿椭圆轨道运动时,卫星所受万有引力不是完全提供卫星的向心力,故卫星中宇航员始终处于完全失重状态是错误的.
故选AC.
点评:卫星绕地球运动,轨道高度越大,发射速度越大,发射越困难,卫星在近地点的速度越大.在随圆轨道上运动的卫星,万有引力和卫星运动所需要向心力不是始终相等的,故在椭圆轨道上运动的卫星不是始终处于完全失重状态.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
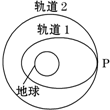 (2010?德州一模)我国于2010年1月17日凌晨在西昌成功发射第三颗北斗导航卫星,此前,我国已成功发射了两颗北斗导航卫星,这次发射的北斗导航卫星(COMPASS-G2)是一颗地球同步卫星.如图所示,假若第三颗北斗导航卫星先沿椭圆轨道1飞行,后在远地点P处点火加速,由椭圆轨道1变成地球同步圆轨道2.下列说法正确的是( )
(2010?德州一模)我国于2010年1月17日凌晨在西昌成功发射第三颗北斗导航卫星,此前,我国已成功发射了两颗北斗导航卫星,这次发射的北斗导航卫星(COMPASS-G2)是一颗地球同步卫星.如图所示,假若第三颗北斗导航卫星先沿椭圆轨道1飞行,后在远地点P处点火加速,由椭圆轨道1变成地球同步圆轨道2.下列说法正确的是( ) 我国于2010年1月17日在西昌成功发射第三颗北斗导航卫星,此前,我国已成功发射了两颗北斗导航卫星,这次发射的北斗导航卫星是一颗地球同步卫星.如图所示,假若第三颗北斗导航卫星先沿椭圆轨道1飞行,后在远地点P处点火加速,由椭圆轨道1变成地球同步圆轨道2.下列说法正确的是( )
我国于2010年1月17日在西昌成功发射第三颗北斗导航卫星,此前,我国已成功发射了两颗北斗导航卫星,这次发射的北斗导航卫星是一颗地球同步卫星.如图所示,假若第三颗北斗导航卫星先沿椭圆轨道1飞行,后在远地点P处点火加速,由椭圆轨道1变成地球同步圆轨道2.下列说法正确的是( )