题目内容
如图31-1所示,从阴极K射出的电子经U0=5000V的电势差加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之间。在离金属板边缘L2=75cm处放置一个直径D=20cm,带有记录纸的圆筒。整个装置放在真空内,电子发射的初速度不计。
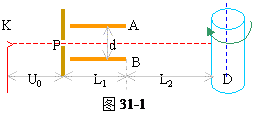
(1)若在金属板上加以U1=1000V的直流电压(A板电势高)后,为使电子沿入射方向作匀速直线运动到达圆筒,应加怎样的磁场(大小和方向);
(2)若在两金属板上加以U2=1000cos2πtV的交流电压,并使圆筒绕中心轴按图示方向以n=2转/秒匀速转动。试确定电子在记录纸上的轨迹形状,并画出1秒钟内所记录到的图形。

(1)若在金属板上加以U1=1000V的直流电压(A板电势高)后,为使电子沿入射方向作匀速直线运动到达圆筒,应加怎样的磁场(大小和方向);
(2)若在两金属板上加以U2=1000cos2πtV的交流电压,并使圆筒绕中心轴按图示方向以n=2转/秒匀速转动。试确定电子在记录纸上的轨迹形状,并画出1秒钟内所记录到的图形。
(1)为使电子作匀速直线运动,应使电子所受电场力与洛仑兹力平衡,即: B=6×10-4T方向为垂直于纸面向里。
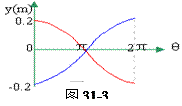
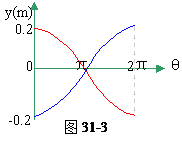
(2)因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。

(2)因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。
偏转极板上加恒定电压 U后,电子在电场中受到恒定的电场力作用,故所加的磁场方向只要使运动电子所受到的洛仑兹力与电场力等大反向即可。偏转极板上加上正弦交流电后,板间电场变为交变电场,电子在板间的运动是水平方向作匀速直线运动,竖直方向作简谐运动。偏出极板后作匀速直线运动,电子到达圆筒后,在筒上留下的痕迹是电子在竖直方向的“扫描”和圆筒匀速转动的合运动。
据动能定理:eU0=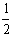 mV02,得电子加速后的入射速度为:
mV02,得电子加速后的入射速度为:
V0=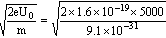 =4.2×107m/s
=4.2×107m/s
(1)加直流电压时,A、B两板间场强:
E1=U1/d=1000/(4×10-2)=2.5×104v/m
为使电子作匀速直线运动,应使电子所受电场力与洛仑兹力平衡,即:qE1=qBV0,
得:B=E1/V0=(2.5×104)/(4.2×107)=6×10-4T
方向为垂直于纸面向里。
(2)加上交流电压时,A、B两板间场强为:E2=U2/d=1000cos2πt/(4×10-2)=2.5×104cos2πt v/m
电子飞离金属板时的偏距为:y1=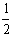 at12=
at12=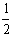 (eE2/m)(L1/V0)2
(eE2/m)(L1/V0)2
电子飞离金属板时的竖直速度为:Vy=at1=(eE2/m)(L1/V0)
从飞离板到到达筒的偏距:y2=Vyt2=(eE2/m)(L1/V0)(L2/V0)=(eE2L1L2)/(mV02)
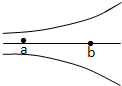
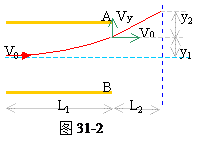
所以在纸筒上的落点对入射方向的总偏距为:(如图31-2所示)
y=y1+y2=(L1/2+L2)(eE2L1/mV02)=(L1/2+L2)(L1U2/2U0d)
=(10/2+75)×10-2×(10×1000cos2πt)/(2×5000×4)="0.20cos2πt" m
可见,在记录纸上的点以振幅0.20m,周期T=2π/ω=1秒而作简谐运动。因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。


据动能定理:eU0=
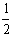 mV02,得电子加速后的入射速度为:
mV02,得电子加速后的入射速度为:V0=
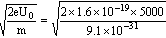 =4.2×107m/s
=4.2×107m/s(1)加直流电压时,A、B两板间场强:
E1=U1/d=1000/(4×10-2)=2.5×104v/m
为使电子作匀速直线运动,应使电子所受电场力与洛仑兹力平衡,即:qE1=qBV0,
得:B=E1/V0=(2.5×104)/(4.2×107)=6×10-4T
方向为垂直于纸面向里。
(2)加上交流电压时,A、B两板间场强为:E2=U2/d=1000cos2πt/(4×10-2)=2.5×104cos2πt v/m
电子飞离金属板时的偏距为:y1=
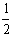 at12=
at12=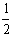 (eE2/m)(L1/V0)2
(eE2/m)(L1/V0)2电子飞离金属板时的竖直速度为:Vy=at1=(eE2/m)(L1/V0)
从飞离板到到达筒的偏距:y2=Vyt2=(eE2/m)(L1/V0)(L2/V0)=(eE2L1L2)/(mV02)
所以在纸筒上的落点对入射方向的总偏距为:(如图31-2所示)
y=y1+y2=(L1/2+L2)(eE2L1/mV02)=(L1/2+L2)(L1U2/2U0d)
=(10/2+75)×10-2×(10×1000cos2πt)/(2×5000×4)="0.20cos2πt" m
可见,在记录纸上的点以振幅0.20m,周期T=2π/ω=1秒而作简谐运动。因圆筒每秒转2周(半秒转1周),故在1秒内,纸上的图形如图31-3所示。

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目