题目内容
9.一列车由等长的车厢连接而成.车厢之间的间隙忽略不计,一人站在站台上与第一节车厢的最前端相齐.当列车由静止开始做匀加速直线运动时开始计时,测量得第1节车厢通过的时间为2s,则从第4节到第16节车厢通过他的时间为多少?分析 取车为参考系,把车的运动转化为人做匀加速直线运动,结合位移时间公式求出人通过前3节车厢和前16节车厢所用的时间,从而得出第4节至第16节车厢通过的时间.
解答 解:取车为参考系,把车的运动转化为人做匀加速直线运动.设每节车厢长为L,加速度为a,则由L=$\frac{1}{2}a{t}_{1}^{2}$,得人通过第一节车厢的时间为:
t1=$\sqrt{\frac{2L}{a}}$=2s,
人通过前3节车厢的时间为:
t3=$\sqrt{\frac{2×3L}{a}}$=2$\sqrt{3}$s
人通过前16节车厢的时间为:
t16=$\sqrt{\frac{2L×16}{a}}$=8s.
故所求的时间为:
△t=t16-t3=(8-2$\sqrt{3}$)s.
答:从第4节到第16节车厢通过他的时间为(8-2$\sqrt{3}$)s.
点评 解决本题的关键在于合理地选择参考系,转化为人做匀加速直线运动,结合位移时间公式进行求解.

练习册系列答案
相关题目
19. 如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程中,下列说法正确的是( )
如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程中,下列说法正确的是( )
 如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程中,下列说法正确的是( )
如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对静止这一过程中,下列说法正确的是( )| A. | 电动机做的功为$\frac{1}{2}$mv2 | B. | 摩擦力对物体做的功为mv2 | ||
| C. | 传送带克服摩擦力做的功为$\frac{1}{2}$mv2 | D. | 电动机增加的功率为μmgv |
20.各行星的运动近似看作匀速圆周运动,则离太阳越远的行星( )
| A. | 周期越小 | B. | 线速度越小 | C. | 角速度越大 | D. | 向心加速度越小 |
17.质量为m的物体,在水平力F作用下,在粗糙的水平面上向右运动.如图所示,下列说法正确的是( )

| A. | 如果物体做匀速直线运动,F一定对物体不做功 | |
| B. | 如果物体做减速直线运动,F一定对物体做负功 | |
| C. | 如果物体做减速直线运动,F一定对物体做正功 | |
| D. | 如果物体做匀速直线运动,合力一定对物体做正功 |
14.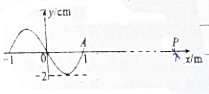 某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
 某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )
某介质中形成一列简谐波t=0时刻的波形如图中实线所示,若波向右传播,零时刻波刚好传到坐标位置为1m处的A点,且再经过0.7s,坐标7m处的P点第一次通过平衡位置并向上振动,则下列说法正确的是( )| A. | 该列波的传播速度为$\frac{60}{7}$m/s | |
| B. | 这列波的周期为$\frac{7}{30}$s | |
| C. | 从t=0时刻其到P点第一次达到波峰停止,O点对平衡位置的位移y0=-2cm | |
| D. | 从t=0时刻起到P点的第一次到达波峰时止,O点所经过的路程S0=0.3m | |
| E. | 该波遇到的频率为5Hz的机械波可发生干涉现象 |
18.下列说法正确的是( )
| A. | 布朗运动是液体分子的无规则运动 | |
| B. | 分子间引力总是随着分子间的距离减小而减小 | |
| C. | 水的饱和汽压随温度的升高而增大 | |
| D. | 分子热运动越剧烈,物体内每个分子的动能越大 | |
| E. | 物体的内能跟物体的温度和体积有关 | |
| F. | 对某物体做功,必定会使该物体的内能增加 | |
| G. | 可以从单一热源吸收热量,使之完全变为功 | |
| H. | 不可能使热量从低温物体传向高温物体 | |
| I. | 功转变为热的实际宏观过程是不可逆过程 | |
| J. | 相对湿度是指空气中实际所含水蒸汽压强和同温度下饱和水蒸汽压强的百分比值 |
19.下列说法正确的是( )
| A. | 中国神舟五号宇宙飞船在酒泉卫星发射中心成功发射,把中国第一位航天员杨利伟送入太空 | |
| B. | 地球的同步卫星运行的轨道与赤道都在同一平面内,并且距地面的高度相同 | |
| C. | 牛顿发现了万有引力定律并测定了引力常量 | |
| D. | 绕地球做匀速圆周运动人造地球卫星的线速度可能大于7.9km/s |
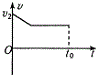
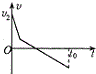
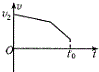
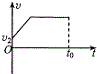
 如图所示,倾斜传送带以速度v1顺时针匀速运动,t=0时刻小物体从底端以速度v2冲上传送带,t=t0时刻离开传送带,下列描述小物体的速度随时间变化的图象可能正确的是( )
如图所示,倾斜传送带以速度v1顺时针匀速运动,t=0时刻小物体从底端以速度v2冲上传送带,t=t0时刻离开传送带,下列描述小物体的速度随时间变化的图象可能正确的是( )