题目内容
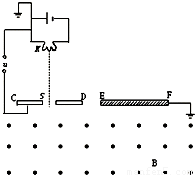
 如图所示的装置,灯丝K发出的所有电子,经过u=Umsinωt+U0的电压加速后 (U0>Um保证电子被加速),从小孔S进入磁感应强度为B的垂直于纸面向外的匀强磁场中,偏转后都能打在萤光屏EF上使它发出萤光,EF与加速电极CD在同一条直线上.若电子在加速电场中运动的时间极短,远远小于2π/ω,电子离开灯丝时的初速度为零,电子的电量为e,质量为m.求EF发光部分的长度?
如图所示的装置,灯丝K发出的所有电子,经过u=Umsinωt+U0的电压加速后 (U0>Um保证电子被加速),从小孔S进入磁感应强度为B的垂直于纸面向外的匀强磁场中,偏转后都能打在萤光屏EF上使它发出萤光,EF与加速电极CD在同一条直线上.若电子在加速电场中运动的时间极短,远远小于2π/ω,电子离开灯丝时的初速度为零,电子的电量为e,质量为m.求EF发光部分的长度?分析:电子在电场中加速,根据动能定理可以求得电子的速度的大小,电子在磁场中运动时,洛伦兹力做为向心力,求出半径的最大和最小值即可.
解答:解:由于电子在加速电场中时间远远小于
,可认为被恒压加速,设在加速电压u作用后,获得速度v,有
ue=
mv2 (1)
进入磁场后,在洛伦兹力作用下偏转,有
evB=m
(2)
故有R=
(3)
当u最大时,R有最大值,u最大值为U0+Um
所以Rmax=
(4)
同理 Rmin=
(5)
发光部分长度d=2Rmax-2Rmin=
(
-
) (6)
答:EF发光部分的长度为
(
-
).
| 2π |
| ω |
ue=
| 1 |
| 2 |
进入磁场后,在洛伦兹力作用下偏转,有
evB=m
| v2 |
| R |
故有R=
| 1 |
| B |
|
当u最大时,R有最大值,u最大值为U0+Um
所以Rmax=
| 1 |
| B |
|
同理 Rmin=
| 1 |
| B |
|
发光部分长度d=2Rmax-2Rmin=
| 2 |
| B |
|
| U0+Um |
| U0-Um |
答:EF发光部分的长度为
| 2 |
| B |
|
| U0+Um |
| U0-Um |
点评:电压不同的时候,电子的速度不同,在磁场中的半径也就不同,最大和最小半径之间的即为发光的区域.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目