Question

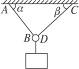
如图3-5-12所示，用AB和CD两根绳悬挂一小轻环，A、C两点在同一水平面上，AC=50 cm，AB=30 cm，绳AB最多能承受5 N的拉力；CD=40 cm，绳CD最多能承受4 N的拉力，问小环下端最多能悬挂多重的物体？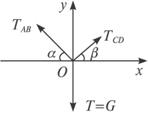

图3-5-12

Answer 1

思路解析：首先应判断AB、CD绳哪个先断，然后按照容易断的绳所能承受的最大拉力来计算G.以绳AB与CD的结点(小环)为研究对象，其受力情况如下图所示：重物对结点的拉力，其大小T＝G；绳AB、CD的拉力设为T_AB、T_CD.由几何关系知sinα＝0.8，cosα=0.6,sinβ＝0.6，cosβ=0.8

根据共点力平衡条件，有：T_CDcosβ-T_ABcosα＝0                             ①

T_CDsinβ+T_ABsinα-G＝0                                                   ②

由式①解得T_AB=43T_CD

讨论：(1)当T_CD＝4 N时，T_AB＝N＞5 N，说明绳AB已断；

(2)当T_AB＝5 N时，T_CD=＜4 N，说明当绳AB受5 N拉力时G最大且两绳均不断.因此，由式②可得：G＝T_ABsinα+T_CDsinβ＝6.25 N.

答案：6.25 N