题目内容
（18分）如图，半径为R的圆是一圆柱形匀强磁场区域的横截面（纸面），磁感应强度大小为B，方向垂直于纸面向里。一带正电荷的粒子沿图中直线以速率v0从圆上的a点射入柱形区域，从圆上b点射出（b点图中未画）磁场时速度方向与射入时的夹角为60°。已知圆心O到直线的距离为
。现将磁场换为平行于纸面且垂直于直线的匀强电场，同一粒子以同样速度沿直线从a点射入柱形区域，也在b点离开该区域。不计重力，求：
（1）粒子的比荷（电荷与质量的比值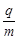
）；
（2）电场强度的大小。
。现将磁场换为平行于纸面且垂直于直线的匀强电场，同一粒子以同样速度沿直线从a点射入柱形区域，也在b点离开该区域。不计重力，求：（1）粒子的比荷（电荷与质量的比值
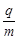）；（2）电场强度的大小。
（1）
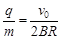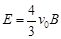
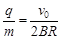；（2）
；（2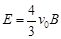）试题分析：（1）（10分）粒子在磁场中做圆周运动。设圆周半径为r，由牛顿第二定律和洛仑兹力公式得
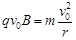①（2分）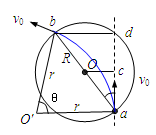
大致画出b点位置及粒子运动轨迹，轨迹圆的圆心为O'，连接ab及O'a、O'b，由题知半径转过的圆心角θ=60°，ΔO'ab为等边三角形，∠O'ab=60°，则∠bac=30°，其中Oc为入射线的垂线段，而在ΔOac中，因
，
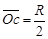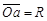，所以∠Oac=30°，即O点在ab连线上。（3分）由几何关系知：r=2R ②（2分）
由①②两式解得：
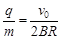③（3分）（2）（8分）考虑粒子在电场中的运动。设电场强度的大小为E，粒子在电场中做类平抛运动。设其加速度大小为a，由牛顿第二定律和带电粒子在电场中的受力公式得qE="ma" ④（2分）
由于ab是圆的直径，入射方向与圆交于d点，则有bd垂直于ad，则ad长度为粒子在垂直于电场方向的位移，bd为粒子在平行于电场方向的位移。由运动学公式得
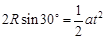⑤（2分）2Rcos30°=v0t ⑥（2分）
由③④⑤⑥解得
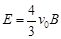（2分）
练习册系列答案
名校课堂系列答案
相关题目
T（圆心在挡板所在垂线上，图中未画出），求所加圆形磁场的面积和离子在磁场区域运动的时间。（计算结果全部保留二位有效数字）
的带负电粒子以速度v0=8×105m/s从两板中间沿与板平行的方向射入偏转电场，若从该粒子进入偏转电场时开始计时，板间场强恰好按图乙所示的规律变化，粒子离开偏转电场后进入匀强磁场并最终垂直磁场右边界射出。不计粒子重力，
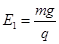，第四象限内电场强度大小为
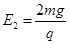；另有一个质量为m，带电量为q（q>0）的小球B从第二象限内的某点由静止释放，当它的运动方向变为水平方向时恰与A相撞，碰撞过程系统损失了
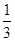的能量，B球电荷量不变。碰后A获得沿x轴正向的速度，最后停止在P点；B球反弹后最后也打在P点。求：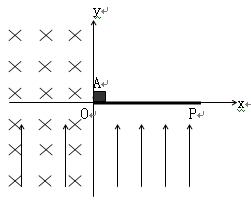
，板间加上一定的电压．现从左端沿中心轴线方向入射一个质量为m、带电量为+q的带电微粒，射入时的初速度大小为v0．一段时间后微粒恰好从下板边缘P1射出电场，并同时进入正三角形区域．已知正三角形区域内存在垂直纸面向里的匀强磁场B1，三角形的上顶点A与上金属板平齐，底边BC与金属板平行．三角形区域的右侧也存在垂直纸面向里、范围足够大的匀强磁场B2，且B2=4B1．不计微粒的重力，忽略极板区域外部的电场．
。离子重力不计。求：