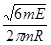题目内容
有一回旋加速器,内部抽成真空,极板间所加交变电压的频率为1.2×106 Hz,半圆形电极的半径为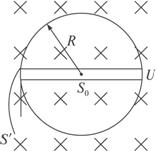
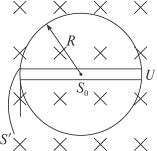
图15-27
(1)加速氘核所需的磁场的磁感应强度多大?
(2)加速后氘核从D形盒中射出时的最大动能是多大?
(3)设加速电压为U=1 000 V,且两极板间距离d=
解析:(1)回旋加速器中所加交变电压的频率f,与带电粒子做匀速圆周运动的频率相等;
f=![]() ,B=
,B=![]() =0.155 T.
=0.155 T.
(2)回旋加速器最后使粒子得到的动能为:Ek=![]() mv2=
mv2=![]() =2mπ
=2mπ
(3)氘核每加速一次所获得的能量为qU,所以共加速的次数为:
N=![]() =164.5=165(次)
=164.5=165(次)
带电粒子在电场中的加速时间可以根据动量定理求得
![]() ·t1=mv-0
·t1=mv-0
即t1=![]() ·d=8.25×10-7 s
·d=8.25×10-7 s
带电粒子在磁场中做匀速圆周运动的时间:
t=(N-1)![]() =
=![]() =6.8×10-5 s
=6.8×10-5 s
t总≈6.88×10-5 s.
答案:(1)0.155 T (2)2.63×10-14 J (3)6.88×10-5 s

练习册系列答案
相关题目
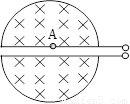
 回旋加速器的核心部分是两个半径为R的D型金属扁盒,如图,盒正中央开有一条窄缝,在两个D型盒之间加交变电压,于是在缝隙中形成交变电场,由于屏蔽作用,在D型盒内部电场很弱,D型盒装在真空容器中,整个装置放在巨大电磁铁的两极之间,磁场方向垂直于D型盒的底面,只要在缝隙中的交变电场的频率不变,便可保证粒子每次通过缝隙时总被加速,粒子的轨道半径不断增大,并逐渐靠近D型盒边缘,加速到最大能量E后,再用特殊的装置将它引出.在D型盒上半面中心出口A处有一正离子源,正离子所带电荷量为q、质量为m,加速时电极间电压大小恒为U.(加速时的加速时间很短,可忽略;正离子从离子源出发时初速为零).则下列说法正确的是( )
回旋加速器的核心部分是两个半径为R的D型金属扁盒,如图,盒正中央开有一条窄缝,在两个D型盒之间加交变电压,于是在缝隙中形成交变电场,由于屏蔽作用,在D型盒内部电场很弱,D型盒装在真空容器中,整个装置放在巨大电磁铁的两极之间,磁场方向垂直于D型盒的底面,只要在缝隙中的交变电场的频率不变,便可保证粒子每次通过缝隙时总被加速,粒子的轨道半径不断增大,并逐渐靠近D型盒边缘,加速到最大能量E后,再用特殊的装置将它引出.在D型盒上半面中心出口A处有一正离子源,正离子所带电荷量为q、质量为m,加速时电极间电压大小恒为U.(加速时的加速时间很短,可忽略;正离子从离子源出发时初速为零).则下列说法正确的是( )| A、增大交变电压U,则正离子在加速器中运行时间将变短 | ||||||||
| B、增大交变电压U,则正离子在加速器中运行时间将不变 | ||||||||
C、正离子第n次穿过窄缝前后的速率之比为
| ||||||||
D、回旋加速器所加交变电压的频率为
|