题目内容
 如图所示,A和B为两个紧靠在一起的硬质橡胶轮,两轮的半径之比RA:RB=3:1. A转动时带动B一起转动(转动过程中两轮间无打滑现象),两轮的角速度之比ωA:ωB=
如图所示,A和B为两个紧靠在一起的硬质橡胶轮,两轮的半径之比RA:RB=3:1. A转动时带动B一起转动(转动过程中两轮间无打滑现象),两轮的角速度之比ωA:ωB=1:3
1:3
,两轮的边缘向心加速度之比aA:aB=1:3
1:3
.分析:本题在皮带轮中考查了线速度、角速度、半径等之间的关系,解决这类问题的关键是弄清哪些地方线速度相等,哪些位置角速度相等.
解答:解:传动过程中,皮带不打滑,说明A、B两点的线速度相等,即vA=vB
根据ω=
得,ω与R成反比,即为ωA:ωB=1:3,
根据a=
,得a与R成反比,即为aA:aB=1:3;
故答案为:1:3;1:3
根据ω=
| v |
| R |
根据a=
| v2 |
| R |
故答案为:1:3;1:3
点评:对于皮带传动装置问题要把握两点一是同一皮带上线速度相等,二是同一转盘上角速度相等.

练习册系列答案
相关题目
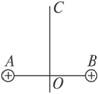
如图所示,A和B为两等量异种电荷,A带正电,B带负电.在A、B的连线上有a、b、c三点,其中b为连线的中点,a、c两点与b点等距,则下列说法错误的( )
| A.a点与c点的电场强度相同 |
| B.a点与c点的电势相同 |
| C.a、b间的电势差与b、c间的电势差相同 |
| D.b点的电场强度与电势均为零 |
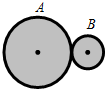 如图所示,A和B为两个紧靠在一起的硬质橡胶轮,两轮的半径之比RA:RB=3:1.A转动时带动B一起转动(转动过程中两轮间无打滑现象),两轮的线速度之比vA:vB=
如图所示,A和B为两个紧靠在一起的硬质橡胶轮,两轮的半径之比RA:RB=3:1.A转动时带动B一起转动(转动过程中两轮间无打滑现象),两轮的线速度之比vA:vB=