题目内容
 (2011?闵行区二模)如图,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:
(2011?闵行区二模)如图,箱子A连同固定在箱子底部的竖直杆的总质量为M=10kg.箱子内部高度H=3.75m,杆长h=2.5m,另有一质量为m=2kg的小铁环B套在杆上,从杆的底部以v0=10m/s的初速度开始向上运动,铁环B刚好能到达箱顶,不计空气阻力,g取10m/s2.求:(1)在铁环沿着杆向上滑的过程中,所受到的摩擦力大小为多少?
(2)在给定的坐标中,画出铁环从箱底开始上升到第一次返回到箱底的过程中箱子对地面的压力随时间变化的图象(可写出简要推算步骤)
(3)若铁环与箱底每次碰撞都没有能量损失,求小环从开始运动到最终停止在箱底,所走过的总路程是多少?
分析:(1)对小铁环上升的过程运用动能定理即可求解;
(2)第一次到达杆顶用时t1,速度为v1,第一次离开杆顶到返回杆顶用时t2,第一次滑到杆底速度为v2,在杆上滑下用时t3
根据运动学基本公式求出时间,再根据牛顿第二定律求出各时间段对应的压力,即可画图;
(3)先求出小环能升到杆顶所需要的能量和小环第一次滑到杆底的机械能,判断是否能再次越过杆顶,再根据动能定理求出在杆上反复滑行的总路程即可求解.
(2)第一次到达杆顶用时t1,速度为v1,第一次离开杆顶到返回杆顶用时t2,第一次滑到杆底速度为v2,在杆上滑下用时t3
根据运动学基本公式求出时间,再根据牛顿第二定律求出各时间段对应的压力,即可画图;
(3)先求出小环能升到杆顶所需要的能量和小环第一次滑到杆底的机械能,判断是否能再次越过杆顶,再根据动能定理求出在杆上反复滑行的总路程即可求解.
解答:(1)对小铁环上升的过程运用动能定理得:
-mgH-fs=0-
mv02
解得:f=10N
(2)第一次到达杆顶用时t1,速度为v1,第一次离开杆顶到返回杆顶用时t2,
第一次滑到杆底速度为v2,在杆上滑下用时t3
v1=
=5m/s
t1=
=
s
t2=
=1s
由动能定理:mgH-fh=mv22
v2=5
m/s
t3=
=(
-1)s=0.41s
图上画出
对0~
s:N1=Mg-f=90N
s~
s:N2=Mg=100N
s~(
+
)s:N3=Mg+f=110N
如下图所示;
 (2)小环能升到杆顶所需要的能量为:
(2)小环能升到杆顶所需要的能量为:
E0=mgh+fh=2×10×2.5+10×2.5=75J
小环第一次滑到杆底的机械能为E2:E2=mv02-2fh=50J
E2<E0所以小环只能越过杆顶一次,
设小环在杆上反复滑行的总路程为s:
有动能定理得:
fs=
mv02
解得:s=10m
s总=2(H-h)+s=12.5m
答:(1)在铁环沿着杆向上滑的过程中,所受到的摩擦力大小为10N;
(2)如图所示;
(3)小环从开始运动到最终停止在箱底,所走过的总路程为12.5m.
-mgH-fs=0-
| 1 |
| 2 |
解得:f=10N
(2)第一次到达杆顶用时t1,速度为v1,第一次离开杆顶到返回杆顶用时t2,
第一次滑到杆底速度为v2,在杆上滑下用时t3
v1=
| 2g(H-H) |
t1=
| 2h |
| v1+v0 |
| 1 |
| 3 |
t2=
| 2v1 |
| g |
由动能定理:mgH-fh=mv22
v2=5
| 2 |
t3=
| 2h |
| v1+v2 |
| 2 |
图上画出
对0~
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
如下图所示;
 (2)小环能升到杆顶所需要的能量为:
(2)小环能升到杆顶所需要的能量为:E0=mgh+fh=2×10×2.5+10×2.5=75J
小环第一次滑到杆底的机械能为E2:E2=mv02-2fh=50J
E2<E0所以小环只能越过杆顶一次,
设小环在杆上反复滑行的总路程为s:
有动能定理得:
fs=
| 1 |
| 2 |
解得:s=10m
s总=2(H-h)+s=12.5m
答:(1)在铁环沿着杆向上滑的过程中,所受到的摩擦力大小为10N;
(2)如图所示;
(3)小环从开始运动到最终停止在箱底,所走过的总路程为12.5m.
点评:本题主要考查了动能定理的直接应用,在第(3)问中要注意先判断小环能离开杆顶几次,铁环与箱底每次碰撞都没有能量损失,说明速度大小不变,方向相反,难度适中.

练习册系列答案
相关题目
 (2011?闵行区二模)如图所示,一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭,上端足够长,下端(粗端)中间有一段水银封闭了一定质量的理想气体.现对气体缓慢加热,气体温度不断升高,水银柱上升,则被封闭气体体积和热力学温度的关系最接近哪个图象( )
(2011?闵行区二模)如图所示,一根上细下粗、粗端与细端都粗细均匀的玻璃管上端开口、下端封闭,上端足够长,下端(粗端)中间有一段水银封闭了一定质量的理想气体.现对气体缓慢加热,气体温度不断升高,水银柱上升,则被封闭气体体积和热力学温度的关系最接近哪个图象( )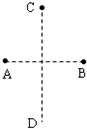 (2011?闵行区二模)如图所示,两个等量同种点电荷分别固定于光滑绝缘水平面上A、B两点.一个带电粒子由C点静止释放,仅受电场力作用,沿着AB中垂线从C点运动到D点(C、D是关于AB对称的两点).下列关于粒子运动的v-t图象中可能正确的是( )
(2011?闵行区二模)如图所示,两个等量同种点电荷分别固定于光滑绝缘水平面上A、B两点.一个带电粒子由C点静止释放,仅受电场力作用,沿着AB中垂线从C点运动到D点(C、D是关于AB对称的两点).下列关于粒子运动的v-t图象中可能正确的是( )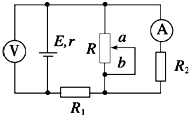 (2011?闵行区二模)电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )
(2011?闵行区二模)电动势为E、内阻为r的电源与定值电阻R1、R2及滑动变阻器R连接成如图所示的电路,当滑动变阻器的触头由中点滑向b端时,下列说法正确的是( )