题目内容
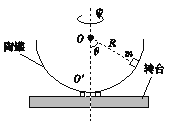
【题目】如图所示，在内壁光滑的平底试管内放一个质量为1g的小球，试管的开口端与水平轴O连接，试管底与O相距5cm，试管在转轴带动下在竖直平面内做匀速圆周运动。g取10m/s。求：
(1)要使小球始终不脱离试管底部，转轴的角速度至少为多大?(结果可以用根式表示)
(2)转轴的角速度达到多大时，转动一周的过程中，试管底所受压力的最大值等于最小值的3倍?
【答案】(1) 
(2) 
【解析】试题分析：小球在最高点时压力最小，在最低点时，压力最大，根据牛顿第二定律求出匀速转动的角速度大小．
（1）当小球对试管的压力正好等于0时，小球刚好与试管分离，根据向心力公式得：
对小球，在最高点有
，解得
；
（2）在最高点，根据牛顿第二定律得， 
，
在最低点，根据牛顿第二定律得， 
， 
，
联立解得
．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
