Question

图（a）所示的xOy平面处于匀强磁场中，磁场方向与xOy平面(纸面)垂直，磁感应强度B随时间t变化的周期为T，变化图线如图（b）所示。当B为+B₀时，磁感应强度方向指向纸外。在坐标原点O有一带正电的粒子P，其电荷量与质量之比恰好等于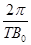。不计重力。设P在某时刻t₀以某一初速度沿y轴正方向自O点开始运动，将它经过时间T到达的点记为A。

（1）若t₀=0，则直线OA与x轴的夹角是多少？

（2）若t₀=T/4，则直线OA与x轴的夹角是多少？

（3）为了使直线OA与x轴的夹角为π/4，在0< t₀< T/4的范围内，t₀应取何值？是多少？

 

Answer 1

【答案】

（1）0（2）（3）

【解析】（1）设粒子P的质量为m，电荷量为q，速度为v，粒子p在洛伦兹力作用下，在xy平面内做圆周运动，用R表示圆周的半径，T’表示运动周期，则有

①

②

由①②式与已知条件得：③

粒子P在t=0到时间内，沿顺时针方向运动半个周期，到达x轴上B点，此时磁场方向反转；继而，在到t=T时间内，沿逆时针方向运动半个圆周，到达x轴上A点，如图（a）所示

OA与x轴的夹角④

（2）粒子P在时刻开始运动，在到时间内，沿顺时针方向运动个圆周，到达C点，此时磁场方向反转；继而，在到t=T时间内，沿逆时针方向运动半个圆周，到达B点，此时磁场再次反转；在t=T到时间内，沿顺时针方向运动个圆周，到达A点，如图（b）所示

由几何关系可知，A点在y轴上，即OA与x轴夹角⑤

（3）若在任意时刻粒子P开始运动，在到时间内，沿顺时针方向运动到达C点，圆心O’位于x轴上，圆弧OC对应的圆心角为⑥

此时磁场方向反转；继而，在到t=T时间内，沿逆时针方向运动半个圆周，到达B点，此时磁场再次反转；在t=T到时间内，沿顺时针方向作圆周运动到达A点，

设圆心为O’’，圆弧BA对应圆心角为，如图（c）所示。

由几何关系可知，C、B均在连线上，且

若要OA与x成角，则有

联立解得