题目内容
1.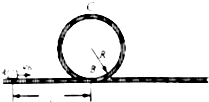 过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=1.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=10m/s的初速度沿轨道向右运动,A、B间距L=9m.小滑块与水平轨道间的动摩擦因数μ=0.20.圆形轨道是光滑的,圆形轨道右侧的水平轨道足够长.取重力加速度g=10m/s2.求:
过山车是游乐场中常见的设施.如图是一种过山车的简易模型,它由水平轨道和在竖直平面内半径R=1.0m的圆形轨道组成,B、C分别是圆形轨道的最低点和最高点.一个质量为m=1.0kg的小滑块(可视为质点),从轨道的左侧A点以v0=10m/s的初速度沿轨道向右运动,A、B间距L=9m.小滑块与水平轨道间的动摩擦因数μ=0.20.圆形轨道是光滑的,圆形轨道右侧的水平轨道足够长.取重力加速度g=10m/s2.求:(1)滑块经过B点时的速度大小vB;
(2)滑块经过C点时受到轨道的作用力大小F;
(3)滑块最终停留点D(图中未画出)与起点A的距离s.
分析 (1)对滑块的运动过程进行分析.从A到B,只有摩擦力做功,根据动能定理得求得小滑块经过B点的速度;
(2)运用动能定理求出滑块经过圆轨道的最高点C时的速度,再对滑块在圆轨道的最高点进行受力分析,并利用牛顿第二定律求出轨道对滑块作用力F.
(3)滑块在整个运动的过程中,摩擦力做功与滑块动能的变化,写出方程即可求得s.
解答 解:(1)从A到B,根据动能定理得:
-μmgL=$\frac{1}{2}$m${v}_{B}^{2}$-$\frac{1}{2}m{v}_{0}^{2}$
代入数据解得:vB=8m/s
(2)从B到C,根据机械能守恒得:
$\frac{1}{2}$m${v}_{B}^{2}$=$\frac{1}{2}m{v}_{C}^{2}$+2mgR
小滑块在最高点时,根据牛顿第二定律得:
mg+F=m$\frac{{v}_{C}^{2}}{R}$
得:F=14N
(3)小滑块在整个运动的过程,根据动能定理得:
-μmgs=0-$\frac{1}{2}m{v}_{0}^{2}$
得:s=$\frac{{v}_{0}^{2}}{2μg}$=25m
答:(1)滑块经过B点时的速度大小vB是8m/s.
(2)滑块经过C点时受到轨道的作用力大小F是14N.
(3)滑块最终停留点D(图中未画出)与起点A的距离s是25m.
点评 本题要灵活选取研究过程,运用动能定理解题.动能定理的优点在于适用任何运动包括曲线运动.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
12.在波的传播方向上,两质点a、b相距1.05m,已知a达到最大位移时,b恰好在平衡位置,若波的频率是200Hz,则波速可能是( )
| A. | 420m/s | B. | 280m/s | C. | 150m/s | D. | 140m/s |
9.2013年6月13日,“神舟十号”飞船与“天宫一号”目标飞行器成功实现自动交会对接,对接轨道所处的空间存在极其稀薄的空气,下面说法正确的是( )
| A. | 为实现对接,两者运行速度的大小都介于第一宇宙速度和第二宇宙速度之间 | |
| B. | 如不加干预.在运行一段时间后,“天宫一号“的动能可能会减少 | |
| C. | 如不加干预,“天宫一号”的轨道高度将缓慢降低 | |
| D. | 航天员在“天宫一号”中不受地球引力作用 |
16.一汽车发动机的额定功率为80kW,汽车在水平路面上以72km/h的速度匀速直线行驶时,受到的阻力大小为2×103N,则这辆汽车匀速行驶时发动机的实际功率为( )
| A. | 40kW | B. | 80kW | C. | 14.4kW | D. | 60kW |
6. 比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
 比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )
比功率是衡量汽车动力性能的一个综合指标,具体是指汽车发动机最大功率与汽车总质量之比,一般来讲,对同类型汽车而言,比功率越大,汽车的动力性越好,普通国产抵挡车大概范围在0.04-0.07kW/kg,中档车的大概范围从0.06-0.10 kW/kg,高档车则更高,范围也更广,大概范围从0.08-0.13kW/kg,为爱了粗略检测一种新汽车的比功率,工程师用速度传感器记录下该汽车在水平道路上,以恒定最大功率从静止开始启动到最大速度过程中的速度图象如图所示,已知从静止开始以恒定功率启动后26s,到达机车的最大速度40m/s,汽车运动过程中阻力不变,则根据比功率来粗略可以判断( )| A. | 这种车可能是国产高档车 | B. | 这种车可能是国产中档车 | ||
| C. | 这种车可能是国产低档车 | D. | 条件不足,不能判断 |
13. 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其p-T图象如图所示.下列判断正确的( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其p-T图象如图所示.下列判断正确的( )
 一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其p-T图象如图所示.下列判断正确的( )
一定量的理想气体从状态a开始,经历三个过程ab、bc、ca回到原状态,其p-T图象如图所示.下列判断正确的( )| A. | 过程ab中气体体积一定增大 | |
| B. | 过程bc中内能不变 | |
| C. | a、b和c三个状态中,状态a分子的平均动能最小 | |
| D. | b和c两个状态的温度相同 |
10.一足球以0.5m/s的速度撞击墙壁,与墙壁作用0.1s后,以0.3m/s的速度反向弹回,以初速度方向为正方向,则足球在与墙壁作用过程中的平均加速度为( )
| A. | -8m/s2 | B. | 8m/s2 | C. | -2m/s2 | D. | 2m/s2 |
 如图是一列简谐波在t=0时刻的波形图,介质中x=4m处质点沿y轴方向做简谐运动的表达式为y=0.2sin5πtcm.关于这列波,下列说法正确的是ABE.
如图是一列简谐波在t=0时刻的波形图,介质中x=4m处质点沿y轴方向做简谐运动的表达式为y=0.2sin5πtcm.关于这列波,下列说法正确的是ABE.