��Ŀ����
����Ŀ����ͼ��ʾ���ڷ�����ֱ���ϡ���СΪE=1��106V/m����ǿ�糡�У��̶�һ������A��B����С����Ϊ�ʵ㣩�Ĺ⻬��ԵԲ����Բ������ֱƽ���ڣ�Բ��ΪO���뾶ΪR=0.2m��A��B��һ����Ե���������A���ĵ����Ϊq=+7��10��7C��B�����磬�����ֱ�ΪmA=0.01kg��mB=0.08kg������С���Բ���ϵ�ͼʾλ�ã�A��Բ��O�ȸߣ�B��Բ��O�����·����ɾ�ֹ�ͷţ���С��ʼ����ʱ�뷽��ת�����������ٶȴ�СΪg=10m/s2��
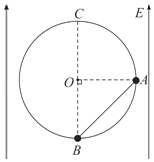
��1��ͨ�������жϣ�С��A�ܷ�Բ������ߵ�C��
��2����С��A������ٶ�ֵ��
��3����С��A��ͼʾλ����ʱ��ת���Ĺ����У�������ܱ仯�����ֵ��
���𰸡���1��A���ܵ���Բ����ߵ� ��2��![]() ��3��0.1344J
��3��0.1344J
�����������������A��B��ת�������У��ֱ��A��B�ɶ��ܶ����з�������ٶȴ�С���ɴ��ж�A�ܲ��ܵ���Բ����ߵ㣻 A��B��Բ���˶��İ뾶�ͽ��ٶȾ���ͬ����A��B�ֱ��ɶ��ܶ����з��������������ٶȣ�A��B��ͼʾλ����ʱ��ת�������У��������ٶ�Ϊ0ʱ�����ݵ����ܵļ�����糡��������ϵ��⡣
��1����A��B��ת�������У���˶�A��B���Ĺ��ֱ�ΪWT��![]() ��
��
������������ ![]()
��A��B����Բ����ߵ�Ķ��ֱܷ�ΪEKA��EKB
��A���ݶ��ܶ�����qER��mAgR+WT1=EKA
��B���ݶ��ܶ����� ![]()
������ã�EKA+EKB=��0.04J
�ɴ˿�֪��A��Բ����ߵ�ʱ��ϵͳ����Ϊ��ֵ����A���ܵ���Բ����ߵ�
��2����Bת������ʱ��A��B���ٶȴ�С�ֱ�ΪvA��vB��
��A��B��Բ���˶��İ뾶�ͽ��ٶȾ���ͬ���ʣ�vA=vB
��A���ݶ��ܶ����� ![]()
��B���ݶ��ܶ����� ![]()
������ã� ![]()
�ɴ˿ɵ�����![]() ʱ��A��B������ٶȾ�Ϊ
ʱ��A��B������ٶȾ�Ϊ![]()
��3��A��B��ͼʾλ����ʱ��ת�������У��������ٶ�Ϊ��ʱ���糡��������࣬�����ܼ�����࣬���Ͽ�ʽ����3sin��+4cos����4=0
��ã� ![]() ��sin��=0����ȥ��
��sin��=0����ȥ��
����A�ĵ����ܼ��٣� ![]()

 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�