题目内容
 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求:
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求:
(1)放上木块后木板的加速度
(2)若要使木块不从木板上滑下来,木板的最小长度.
解:(1)开始时木板的加速度为:
a= =2.5m/s2
=2.5m/s2
4秒末木板的速度为:
v=at=10m/s
放上木块后木板的加速度为:
a1= =0
=0
(2)木块的加速度为:
a2=μ2g=4m/s2
可见4秒后木板做匀速运动,木块做匀加速运动,当木块不从木板上滑下时两者具有相同的速度.
设木块加速到木板的速度时所用的时间为t′,则t′= =2.5s
=2.5s
这段时间内木块相对于木板滑动的距离为L=vt′- at′2=12.5m;
at′2=12.5m;
答:(1)放上木块后木板的加速度为0;
(2)若要使木块不从木板上滑下来,木板的最小长度为12.5m.
分析:(1)放上木块后,木板受重力、压力、支持力、滑块对其向后的滑动摩擦力和地面对其向后的滑动摩擦力,根据牛顿第二定律求解加速度即可;
(2)放木块前,在拉力作用下,木板做匀加速直线运动,根据牛顿第二定律求解加速度,根据运动学公式求解出末速度;通过第一问得到放木块后木板的加速度为零,做匀速直线运动,木块做匀加速直线运动,当两者速度相同时,相对滑动距离最大,根据运动学公式求解出最大相对滑动距离即可.
点评:本题关键是明确滑块和滑板的各段运动过程的运动性质,对于每段过程都要根据牛顿第二定律求解各自的加速度,根据运动学公式求解相关运动参量,还要注意各个过程的连接点的情况.
a=
 =2.5m/s2
=2.5m/s24秒末木板的速度为:
v=at=10m/s
放上木块后木板的加速度为:
a1=
 =0
=0(2)木块的加速度为:
a2=μ2g=4m/s2
可见4秒后木板做匀速运动,木块做匀加速运动,当木块不从木板上滑下时两者具有相同的速度.
设木块加速到木板的速度时所用的时间为t′,则t′=
 =2.5s
=2.5s这段时间内木块相对于木板滑动的距离为L=vt′-
 at′2=12.5m;
at′2=12.5m;答:(1)放上木块后木板的加速度为0;
(2)若要使木块不从木板上滑下来,木板的最小长度为12.5m.
分析:(1)放上木块后,木板受重力、压力、支持力、滑块对其向后的滑动摩擦力和地面对其向后的滑动摩擦力,根据牛顿第二定律求解加速度即可;
(2)放木块前,在拉力作用下,木板做匀加速直线运动,根据牛顿第二定律求解加速度,根据运动学公式求解出末速度;通过第一问得到放木块后木板的加速度为零,做匀速直线运动,木块做匀加速直线运动,当两者速度相同时,相对滑动距离最大,根据运动学公式求解出最大相对滑动距离即可.
点评:本题关键是明确滑块和滑板的各段运动过程的运动性质,对于每段过程都要根据牛顿第二定律求解各自的加速度,根据运动学公式求解相关运动参量,还要注意各个过程的连接点的情况.

练习册系列答案
相关题目
 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求:
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.求: (1)下列说法正确的有
(1)下列说法正确的有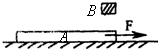 如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.
如图所示,质量显m1=2kg的木板A放在水平面上,木板与水平面间的动摩擦因数为μ1=0.1.木板在F=7N的水平拉力作用下由静止开始向右做匀加速运动,经过时间t=4s时在木板的右端轻放一个质量为m2=1kg的木块B,木块与木板间的动摩擦因数为μ2=0.4.且木块可以看成质点.若要使木块不从木板上滑下来,求木板的最小长度.