题目内容
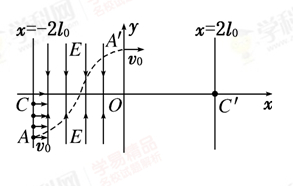
(9分)如图所示,在x轴上方有一竖直向下的匀强电场区域,电场强度为E=500V/m。x轴下方分布有很多磁感应强度为B=1T的条形匀强磁场区域,其宽度均为d1=3cm,相邻两磁场区域的间距为d2=4cm。现将一质量为m=5×10-13kg、电荷量为q=1×10-8C的带正电的粒子(不计重力)从y轴上的某处静止释放,则:
(1)若粒子从坐标(0,h1)点由静止释放,要使它经过x轴下方时,不会进入第二磁场区,h1应满足什么条件?
(2)若粒子从坐标(0,5cm)点由静止释放,求自释放到第二次过x轴的时间(π取3.14)。
(1)1.8×10-2m;(2)3.75×10-4s。
解析试题分析:(1)粒子经电场加速,经过x轴时速度大小为v1,满足:
之后进入下方磁场区,依据题意可知运动半径应满足:R1<d1,又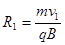
由以上三式可得: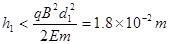 。
。
(2)当粒子从h2=5cm的位置无初速度释放后,先在电场中加速度,
加速时间为t1满足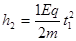 解得
解得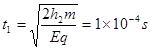

解得
进入磁场的速度大小为v2,圆周运动半径为R2,故
根据粒子在空间运动的轨迹可知,
它最低能进入第二个磁场区它在磁场区运动的总时间为半个周期
它经过第一无磁场区运动方向与x轴正方向的夹角θ满足: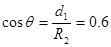
所以它在无磁场区的路程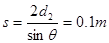
无磁场区运动时间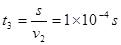
总时间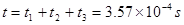
考点:带电粒子在电场与磁场运动的有关计算。

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目



 cm,板长
cm,板长 cm,一个质量为
cm,一个质量为 kg的带电微粒,以
kg的带电微粒,以 m/s的水平初速度从两板间正中央射入,如图所示,取
m/s的水平初速度从两板间正中央射入,如图所示,取 m/s2。
m/s2。
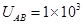 V时,微粒恰好不发生偏转,求微粒的电量和电性。
V时,微粒恰好不发生偏转,求微粒的电量和电性。 的取值范围?
的取值范围?