题目内容
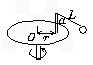
如图, 在水平转台上放一质量为M的木块, 木块与转台间的最大静摩擦因数为μ,它通过细绳与另一木块m相联, 转台以角速度ω转动, M与转台能保持相对静止时, 它到转台中心的最大距离R1和最小距离R2为[ ]
答案：A
解析：
解析：
|
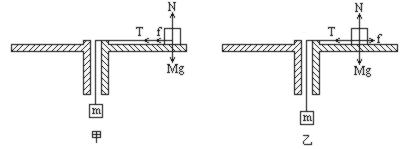
解: 如图甲, M在离中心最大距离R1处受到四力作用: 重力mg,平台的支持力N, 绳的拉力T, 最大静摩擦力f(与T的方向一致). 由m保持静止知, T = mg, 又由M恰好不向外运动知, f = μN = μMg . T和f的合力为木块M作圆周运动的向心力, 即 T + f = mg + μMg = Mω2R1 , 如图乙, M在离中心最小距离R2处, 受到的最大静摩擦力与绳的拉力方向相反, 此时, mg - μMg =Mω2R2
|
练习册系列答案
孟建平错题本系列答案
超能学典应用题题卡系列答案
相关题目
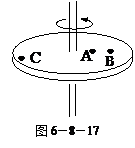
插立一竖直杆
，杆顶系一根长为L的细绳，绳的末端挂一个质量为m的小球，如图所示，当转台匀速转动后，试证悬绳张开的角度α与转台转速n的关系是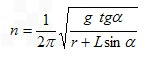
。