题目内容
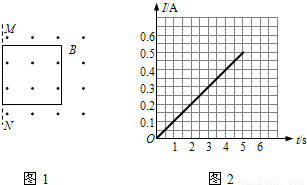
如图所示,边长L=2.5m、质量m=0.50kg的正方形金属线框,放在磁感应强度B=0.80T的匀强磁场中,它的一边与磁场的边界MN重合.在力F作用下由静止开始向左运动,5.0s末时从磁场中拉出.测得金属线框中的电流随时间变化的图象如下图所示.已知金属线框的总电阻R=4.0Ω,求:(1)t=5.0s时金属线框的速度;
(2)t=4.0s时金属线框受到的拉力F的大小;
(3)已知在5.0s内力F做功1.92J,那么金属线框从磁场拉出的过程中,线框中产生的焦耳热是多少.
【答案】分析:(1)由图象求出t=5s时的电流,由F=BLv求出导体棒产生的感应电动势,由欧姆定律求出感应电流,解方程即可求出金属线框的速度.
(2)求出感应电流的表达式,代入数据求出金属框的加速度;由图象求出4s时的感应电流,然后由牛顿第二定律及安培力公式求出拉力.
(3)根据能量守恒定律求出焦耳热.
解答:解:(1)由图可知 t=5s时 线框中电流为0.5A,
此时线框产生的感应电动势E=BLv,
此时线框产生的感应电流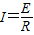 ,
,
带入数据解得:v=1m/s;
(2)由图可知电流I与时间成正比,
感应电流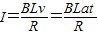 ,
,
所以导线框做匀加速运动,
加速度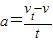 ,
,
带入数据得a=0.2m/s2,
t=4s时,I=0.4A,
由牛顿定律得:F-BIL=ma,
带入数据解得F=0.9N;
(3)由能量守恒定律得: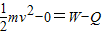 ;
;
解得:Q=1.67J;
答:(1)t=5.0s时金属线框的速度为1m/s;
(2)t=4.0s时金属线框受到的拉力F的大小为0.9N;
(3)线框中产生的焦耳热是1.67J.
点评:由图象求出时间所对应的电流、应用E=BLv、欧姆定律、牛顿第二定律、能量守恒定律即可正确解题.
(2)求出感应电流的表达式,代入数据求出金属框的加速度;由图象求出4s时的感应电流,然后由牛顿第二定律及安培力公式求出拉力.
(3)根据能量守恒定律求出焦耳热.
解答:解:(1)由图可知 t=5s时 线框中电流为0.5A,
此时线框产生的感应电动势E=BLv,
此时线框产生的感应电流
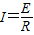 ,
,带入数据解得:v=1m/s;
(2)由图可知电流I与时间成正比,
感应电流
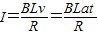 ,
,所以导线框做匀加速运动,
加速度
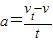 ,
,带入数据得a=0.2m/s2,
t=4s时,I=0.4A,
由牛顿定律得:F-BIL=ma,
带入数据解得F=0.9N;
(3)由能量守恒定律得:
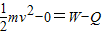 ;
;解得:Q=1.67J;
答:(1)t=5.0s时金属线框的速度为1m/s;
(2)t=4.0s时金属线框受到的拉力F的大小为0.9N;
(3)线框中产生的焦耳热是1.67J.
点评:由图象求出时间所对应的电流、应用E=BLv、欧姆定律、牛顿第二定律、能量守恒定律即可正确解题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 如图所示,边长L=2.5m、质量m=0.50kg的正方形金属线框,放在磁感应强度B=0.80T的匀强磁场中,它的一边与磁场的边界MN重合.在力F作用下由静止开始向左运动,5.0s末时从磁场中拉出.测得金属线框中的电流随时间变化的图象如下图所示.已知金属线框的总电阻R=4.0Ω,求:
如图所示,边长L=2.5m、质量m=0.50kg的正方形金属线框,放在磁感应强度B=0.80T的匀强磁场中,它的一边与磁场的边界MN重合.在力F作用下由静止开始向左运动,5.0s末时从磁场中拉出.测得金属线框中的电流随时间变化的图象如下图所示.已知金属线框的总电阻R=4.0Ω,求: 如图所示,边长L=2.5m、质量m=0.50kg的正方形金属线框总电阻R=4.0Ω,放在磁感应强度B=0.80T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力作用下由静止开始向左运动,经5.0s从磁场中拉出.金属线框中电流I随时间t变化的图象如图所示.
如图所示,边长L=2.5m、质量m=0.50kg的正方形金属线框总电阻R=4.0Ω,放在磁感应强度B=0.80T的匀强磁场中,它的一边与磁场的边界MN重合.在水平力作用下由静止开始向左运动,经5.0s从磁场中拉出.金属线框中电流I随时间t变化的图象如图所示.

