题目内容
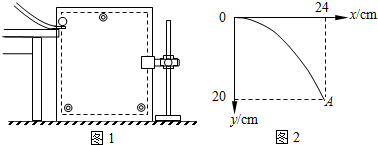
17. 如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )
如图所示,A、B两点分别位于大小两轮O1、O2的边缘上,C点位于大轮O1半径的中点,大轮半径是小轮的2倍,它们之间靠摩擦传动,接触面不打滑.在两轮转动时,对于A、B、C三点的线速度和角速度,以下关系成立的是( )| A. | vA:vB:vC=1:1:1 | B. | vA:vB:vC=1:1:2 | C. | ωA:ωB:ωC=1:1:1 | D. | ωA:ωB:ωC=1:2:1 |
分析 两轮靠摩擦传动,轮子边缘上的点线速度大小相等,共轴转动角速度大小相等,根据v=rω求出角速度大小之比和线速度大小之比.
解答 解:A、点A、点B、点C的转动半径之比为2:1:1,A、B两点在相等时间内通过的弧长相等,则A、B线速度大小相等;A、C两点的角速度大小相等,根据v=rω知,A的线速度是C的2倍;故A、B、C线速度之比为2:2:1,点A和点C的角速度大小相等;点A和点B线速度大小相等,转动半径之比为2:1,根据v=rω知,A、B两点转动的角速度之比为1:2;故A、B、C角速度之比为1:2:1;则有线速度之比为:2:2:1;角速度之比为;1:2:1;故只有D正确;
故选:D.
点评 解决本题的关键知道靠摩擦传到轮子上的各点线速度大小相等,共轴转动的各点角速度大小相等

练习册系列答案
相关题目
7. 如图(a)、(b)所示,当a、b两端与e、f两端分别加上220V的交流电压时,测得c、d间与g、h间的电压均为110V,若分别在c、d两端与g、h两端加上110V的直流电压,则a、b与e、f间的电压为( )
如图(a)、(b)所示,当a、b两端与e、f两端分别加上220V的交流电压时,测得c、d间与g、h间的电压均为110V,若分别在c、d两端与g、h两端加上110V的直流电压,则a、b与e、f间的电压为( )
 如图(a)、(b)所示,当a、b两端与e、f两端分别加上220V的交流电压时,测得c、d间与g、h间的电压均为110V,若分别在c、d两端与g、h两端加上110V的直流电压,则a、b与e、f间的电压为( )
如图(a)、(b)所示,当a、b两端与e、f两端分别加上220V的交流电压时,测得c、d间与g、h间的电压均为110V,若分别在c、d两端与g、h两端加上110V的直流电压,则a、b与e、f间的电压为( )| A. | 0V,220V | B. | 0V,110V | C. | 220V,220V | D. | 220V,110V |
8.根据最新官方消息,中国火星探测任务基本确定,发射时间大致在2018年左右,若火星探测器在登陆火星之前需在靠近火星表面绕火星做匀速圆周运动,已知引力常量为G,则科研人员想估测火星的平均密度,还只需知道探测器在火星表面绕火星做匀速圆周运动时的( )
| A. | 周期 | B. | 轨道的周长 | C. | 探测器的质量 | D. | 线速度的大小 |
5.2009年9月14日,我国海南航天发射场在海南省文昌市破土动工,标志着我国新建航天发射场已进入全面实施阶段.发射场建成使用后,对于优化和完善我国航天发射场布局,推动航天事业可持续发展具有重要战略意义.海南航天发射场主要用于发射新一代大型无毒、无污染运载火箭,承担地球同步轨道卫星、大质量极轨卫星、大吨位空间站和深空探测航天器等航天发射任务,预计于2013年建成并投入使用.这样选址的优点是,在赤道附近( )
| A. | 地球的引力较大 | B. | 重力加速度较大 | ||
| C. | 地球自转角速度较大 | D. | 地球自转线速度较大 |
2.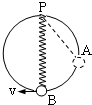 如图所示,有一质量不计劲度系数为k的轻质弹簧,其一端系在竖直放置的半径为R的圆环顶点P,另一端系在质量为m的小球上,小球套在光滑的圆环上,弹簧处于自然状态时小球在A处,A比B高R,当小球从A由静止开始沿光滑圆环滑至最低点B时,速率为v,此时小球对环没有压力,则以下说法错误的是( )
如图所示,有一质量不计劲度系数为k的轻质弹簧,其一端系在竖直放置的半径为R的圆环顶点P,另一端系在质量为m的小球上,小球套在光滑的圆环上,弹簧处于自然状态时小球在A处,A比B高R,当小球从A由静止开始沿光滑圆环滑至最低点B时,速率为v,此时小球对环没有压力,则以下说法错误的是( )
 如图所示,有一质量不计劲度系数为k的轻质弹簧,其一端系在竖直放置的半径为R的圆环顶点P,另一端系在质量为m的小球上,小球套在光滑的圆环上,弹簧处于自然状态时小球在A处,A比B高R,当小球从A由静止开始沿光滑圆环滑至最低点B时,速率为v,此时小球对环没有压力,则以下说法错误的是( )
如图所示,有一质量不计劲度系数为k的轻质弹簧,其一端系在竖直放置的半径为R的圆环顶点P,另一端系在质量为m的小球上,小球套在光滑的圆环上,弹簧处于自然状态时小球在A处,A比B高R,当小球从A由静止开始沿光滑圆环滑至最低点B时,速率为v,此时小球对环没有压力,则以下说法错误的是( )| A. | 小球从A到B过程,只有重力和弹簧的弹力做功,小球的机械能守恒 | |
| B. | 小球从A到B过程,弹簧的弹力做负功,弹簧的弹性势能增加 | |
| C. | 小球经过B点时,弹簧的伸长量为$\frac{m}{k}$(g+$\frac{{v}^{2}}{R}$) | |
| D. | 小球经过B点时,弹簧的弹性势能为mgR-$\frac{1}{2}$mv2 |
6. 如图所示,竖直方向的平行线表示电场线,但未标明方向.一个带电量为q=-10-6C的微粒,仅受电场力的作用,从M点运动到N点时,动能增加了10-4J,则( )
如图所示,竖直方向的平行线表示电场线,但未标明方向.一个带电量为q=-10-6C的微粒,仅受电场力的作用,从M点运动到N点时,动能增加了10-4J,则( )
 如图所示,竖直方向的平行线表示电场线,但未标明方向.一个带电量为q=-10-6C的微粒,仅受电场力的作用,从M点运动到N点时,动能增加了10-4J,则( )
如图所示,竖直方向的平行线表示电场线,但未标明方向.一个带电量为q=-10-6C的微粒,仅受电场力的作用,从M点运动到N点时,动能增加了10-4J,则( )| A. | 该电荷运动的轨迹可能是b | |
| B. | MN两点间的电势差为-100 V | |
| C. | 该电荷从M点运动到N点时电势能增加 | |
| D. | 该电荷从M点由静止开始运动 |
9.质量相等的甲和乙两物体,甲物体放在广州,乙物体放在北京,它们随地球一起转动时,下列说法正确的是( )
| A. | 甲的线速度大,其向心加速度等于重力加速度 | |
| B. | 甲的线速度大,甲和乙与地球自转的周期相等 | |
| C. | 乙的线速度大,甲和乙与地球自转的周期相等 | |
| D. | 甲和乙的线速度相等,均等于第一宇宙速度 |
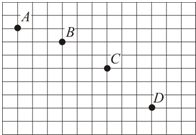 如图所示是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸每一小格的边长为2.5cm,A、B、C、D是同一小球在频闪照相中拍下的四个连续的不同位置时的照片,则
如图所示是某同学用频闪照相研究平抛运动时拍下的照片,背景方格纸每一小格的边长为2.5cm,A、B、C、D是同一小球在频闪照相中拍下的四个连续的不同位置时的照片,则