题目内容
12.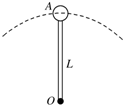 长L=0.5m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个物体A.A的质量为m=2kg,当A通过最高点时,如图所示,求在下列两种情况下杆对小球的力.(g=10m/s2)
长L=0.5m、质量可忽略的细杆,其一端可绕O点在竖直平面内转动,另一端固定着一个物体A.A的质量为m=2kg,当A通过最高点时,如图所示,求在下列两种情况下杆对小球的力.(g=10m/s2)(1)A在最低点的速率为$\sqrt{21}$m/s;
(2)A在最低点的速率为6m/s.
分析 根据动能定理求出球在最高点的速度大小,结合牛顿第二定律求出杆对球的作用力.
解答 解:(1)根据动能定理得,$-2mgL=\frac{1}{2}m{{v}_{1}}^{2}-\frac{1}{2}m{{v}_{0}}^{2}$,
代入数据解得,最高点的速度v1=1m/s,
根据牛顿第二定律得,$mg-{F}_{1}=m\frac{{{v}_{1}}^{2}}{L}$,解得${F}_{1}=20-2×\frac{1}{0.5}N=16N$,方向竖直向上.
(2)根据动能定理得,$-2mgL=\frac{1}{2}m{{v}_{2}}^{2}-\frac{1}{2}m{v}_{0}{′}^{2}$,
代入数据解得最高点的速度v2=4m/s,
根据牛顿第二定律得,$mg+{F}_{2}=m\frac{{{v}_{2}}^{2}}{L}$,解得${F}_{2}=2×\frac{16}{0.5}-20N=44N$.方向竖直向下.
答:(1)A在最低点的速率为$\sqrt{21}$m/s,杆对球的作用力为16N.
(2)A在最低点的速率为6m/s,杆对球的作用力为44N.
点评 本题考查了动能定理和牛顿第二定律的综合运用,知道小球在最高点向心力的来源,结合牛顿第二定律进行求解.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
3.物体在万有引力场中具有的势能叫做引力势能.若取两物体相距无穷远时的引力势能为零,则一个质量为m0的质点到质量为M0的引力源中心的距离为r0时,其万有引力势能为EP=-$\frac{G{M}_{0}{m}_{0}}{{r}_{0}}$(式中G为万有引力常量).一颗质量为m的人造地球卫星沿轨道半径为r1的圆形轨道环绕地球做匀速圆周运动,已知地球的质量为M,要使此卫星绕地球做匀速圆周运动的轨道半径增大为r2,则卫星上的发动机所消耗的最小能量为:(假设卫星的质量始终不变,不计一切阻力及其它星体的影响)( )
| A. | E=$\frac{GMm}{2}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | B. | E=GMm($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | C. | E=$\frac{GMm}{3}$($\frac{1}{{r}_{1}}$-$\frac{1}{{r}_{2}}$) | D. | E=$\frac{2GMm}{3}$($\frac{1}{{r}_{2}}$-$\frac{1}{{r}_{1}}$) |
4.以下关于热现象和热力学规律的描述正确的是( )
| A. | 布朗运动中的颗粒越大,周围液体分子对它碰撞的机会就越大,布朗运动就越显著 | |
| B. | 一定质量的理想气体(分子间的相互作用不计),在绝热膨胀时温度一定降低 | |
| C. | 气体不能无限被压缩,是由于气体分子间距越小时分子斥力越大 | |
| D. | 第二类永动机不能实现,是由于违反了能量转换与守恒定律 |
 如图所示,小木块放置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做功为零,若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做正功.
如图所示,小木块放置于旋转的水平转台上,随转台一起匀速转动,小木块受到的摩擦力对木块做功为零,若小木块随转台一起加速转动而没有相对滑动,则小木块受到的摩擦力对木块做正功.




