题目内容
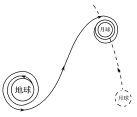
【题目】如图所示，在竖直平面内倾角
的粗糙斜面AB、粗糙水平地面BC、光滑半圆轨道CD平滑对接，CD为半圆轨道的竖直直径。BC长为
，斜面最高点A与地面高度差
，轨道CD的半径
。质量为
的小滑块P从A点静止释放，P与AB、BC轨道间的滑动摩擦因数为
。在C点静止放置一个质量也为的小球Q，P如果能与Q发生碰撞，二者没有机械能损失。已知重力加速度为
，
。求
(1)通过计算判断，滑块P能否与小球Q发生碰撞；
(2)如果P能够与Q碰撞，求碰后Q运动到D点时对轨道的压力大小；
(3)如果小球Q的质量变为
(
为正数)，小球Q通过D点后能够落在斜面AB上，求值范围？
【答案】(1)能；(2)4mg；(3)0＜k＜
【解析】
（1）对P，A到B由动能定理
①
设P能到C点，且速度为
，从B到C同理
②
联立①②式解得
③
④
由 
假设成立，即P能与Q发生碰撞；
（2）对P、Q由碰撞动量守恒
⑤
对P、Q系统能量守恒
⑥
联立③⑤⑥式解得
⑦
对Q球从C到D由动能定理
⑧
对Q球在D点
⑨
又已知
联立⑦⑧⑨⑩式解得
由牛顿第三定律
（3）球Q的质量变为
，同理对P、Q由碰撞动量守恒
⑩
对P、Q系统能量守恒
联立③⑤⑥式得
对Q球从C到D由动能定理
解得
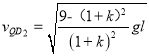
在D点平抛运动，恰好落在Ｂ点，此时对应水平速度为
，有
值范围是
练习册系列答案
相关题目
