题目内容
14．
如图所示，小球质量为m=2kg，大小不计，右边圆轨道半径为R=2m，小球从h=3R处沿斜面滑下后，又沿圆轨道滑到最高点P处，这一过程所用时间为t=10s．求：（1）重力对小球做的功？
（2）重力做功的功率为多大？（g取10m/s2）
分析 根据小球下降的高度求出重力做功的大小，结合运动的时间，根据平均功率公式求出重力做功的功率．
解答 解：（1）整个过程中，重力对小球做功为：
W=mg（3R-2R）=mgR=20×2J=40J．
（2）重力做功的功率为：
$P=\frac{W}{t}=\frac{40}{10}W=4W$．
答：（1）重力对小球做功40J．
（2）重力做功的功率为4W．
点评 解决本题的关键知道重力做功与路径无关，与高度差有关，知道平均功率和瞬时功率的区别，掌握这两种功率的求法．
练习册系列答案
相关题目
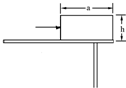如图所示，长为a的薄木板，重为G，放在水平桌面上，开始时长方体右侧面与桌面边缘相齐，现从左侧加一水平力推长木板，使其沿桌面缓慢匀速滑动，设长方体与桌面间的动摩擦因数为μ，那么从开始至长木板下翻，水平力做的功为$\frac{μGa}{2}$．
如图所示，质量m=4.0kg的物体，由高h=0.3m，倾角θ=37°的固定斜面顶端滑到底端．若已知物体与斜面间的动摩擦因数μ=0.2，g取10m/s2．求下滑过程中物体所受外力做的总功．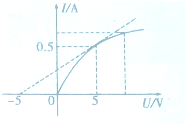
如图所示为某小灯泡的电流与其两端的电压的关系图线，根据电阻的变化规律及所标注的数据，下面有两种计算该小灯泡两端电压为5v时的电阻的方法：
19．对于波长的理解，下列说法正确的是（ ）
| A． | 波动中，对平衡位置的位移总是相等的两个质点间的距离叫波长 | |
| B． | 波动中，对平衡位置的位移总是相等的两个相邻质点间的距离叫波长 | |
| C． | 横波中，只有两个相邻波峰之间的距离等于波长 | |
| D． | 波动中，对平衡位置的位移总是相等的任何两个相邻质点间的距离叫波长 |
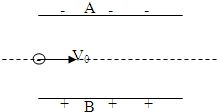有两块带电的平行金属板A、B放在竖直平面内，如图所示，有一个电荷e=-1.6×10-19C，质量为m=2×10-18kg的负电荷，以初速度V0=10m/s水平从平行板中央入射（不考虑重力对运动的影响），已知金属板长L=1m，两板之间距离d=0.1m，两板间的电势差U=10V，求：
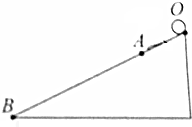伽利略时代，还没有钟表等计时工具，只能用滴水的方法计时，这种滴水计时的装置叫滴水计时器，它每隔相同的时间间隔第一滴水，如图，若从斜面顶端O点处由静止释放小球的同时，有一滴水恰好从滴水计时器的阀门滴下，把这滴水计为第1滴，当小球到斜面的$\frac{1}{4}$处的A点时，第5滴水恰好滴下，那么，小球滚到斜面底端B点时，第几滴水恰好滴下？