题目内容
18.汽车由A地从静止出发,沿平直公路驶向B地,汽车先以加速度a1做匀加速运动,中间做匀速运动,最后以加速度大小a2做匀减速运动,到B地恰好停止,已知A、B两地的路程为x,求汽车驶完全程的最短时间和最大速度.分析 使汽车由A到达B的时间最短,汽车必须没有匀速过程,只有匀加速运动和匀减速运动,即汽车先做匀加速直线运动,后做匀减速直线运动,根据速度公式得到匀加速运动的时间与总时间t的关系,并求出最大速度,根据平均速度公式求出最短时间t.
解答 解:要使列车由A到达B的时间最短,列车必须先匀加速运动,而后立即匀减速运动.
设物体匀加速直线运动和匀减速直线运动的时间分别为t1和t2,最大速度为v.
则有:v=a1t1,v=a2t2
得到 a1t1=a2t2
由数学知识变形得:$\frac{{t}_{2}}{{t}_{1}}=\frac{{a}_{1}}{{a}_{2}}$,
则$\frac{{t}_{1}+{t}_{2}}{{t}_{1}}=\frac{{a}_{1}+{a}_{2}}{{a}_{2}}$,
而t1+t2=t
得到${t}_{1}=\frac{{a}_{2}t}{{a}_{1}+{a}_{2}}$,
则v=a1t1=$\frac{{a}_{1}{a}_{2}t}{{a}_{1}+{a}_{2}}$,
由x=$\frac{v}{2}{t}_{1}+\frac{v}{2}{t}_{2}=\frac{v}{2}t$得,最短时间t=$\sqrt{\frac{2x({a}_{1}+{a}_{2})}{{a}_{1}{a}_{2}}}$,最大速度v=$\sqrt{\frac{2{a}_{1}{a}_{2}x}{{a}_{1}+{a}_{2}}}$.
答:汽车驶完全程的最短时间为$\sqrt{\frac{2x({a}_{1}+{a}_{2})}{{a}_{1}{a}_{2}}}$,最大速度为$\sqrt{\frac{2{a}_{1}{a}_{2}x}{{a}_{1}+{a}_{2}}}$.
点评 本题涉及两个过程的运动学问题,关键要抓住两个过程之间速度联系.也可以运用作速度图象的方法求解.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案| A. | 若A不变,则 a 也不变 | |
| B. | 若A>0且保持不变,则 a 逐渐变小 | |
| C. | 若A不变,则物体在中间位置处的速度为$\frac{{v}_{0}+{v}_{t}}{2}$ | |
| D. | 若A不变,则物体在中间位置处的速度为 $\sqrt{\frac{{{v}_{0}}^{2}+{{v}_{t}}^{2}}{2}}$ |
 利用传感器和计算机可以研究力的大小变化情况,实验时让某同学从桌子上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示该同学受到地面支持力FN随时间变化的图象如图所示.根据图象提供的信息,以下判断错误的是( )
利用传感器和计算机可以研究力的大小变化情况,实验时让某同学从桌子上跳下,自由下落H后双脚触地,他顺势弯曲双腿,他的重心又下降了h.计算机显示该同学受到地面支持力FN随时间变化的图象如图所示.根据图象提供的信息,以下判断错误的是( )| A. | 在0至t2时间内该同学处于失重状态 | |
| B. | 在t2至t3时间内该同学处于超重状态 | |
| C. | t3时刻该同学的加速度为零 | |
| D. | 在t3至t4时间内该同学的重心继续下降 |
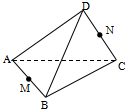 真空中有一正四面体ABCD,如图MN分别是AB和CD的中点.现在A、B两点分别固定电荷量为+Q、-Q的点电荷,下列说法中错误的是( )
真空中有一正四面体ABCD,如图MN分别是AB和CD的中点.现在A、B两点分别固定电荷量为+Q、-Q的点电荷,下列说法中错误的是( )| A. | 将试探电荷+q从C点移到D点,电场力做正功,试探电荷+q的电势能降低 | |
| B. | 将试探电荷-q从M点移到N点,电场力不做功,试探电荷-q的电势能不变 | |
| C. | C、D 两点的电场强度相等 | |
| D. | N点的电场强度方向平行AB且跟CD垂直 |
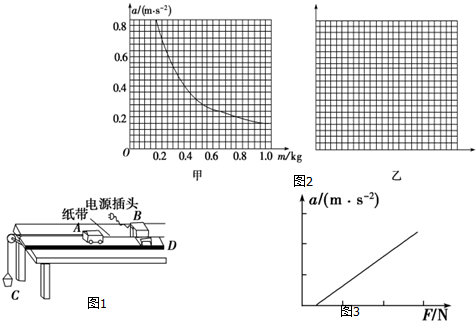
(1)为了消除小车与水平木板之间摩擦力的影响应采取什么做法?平衡摩擦力.
(2)在“探究加速度与质量的关系”时,保持砝码和小桶质量不变,改变小车质量m,分别得到小车加速度a与质量m的数据如下表:
| 次数 | 1 | 2 | 3 | 4 | 5 |
| 小车加速度a/m•s-2 | 0.78 | 0.38 | 0.25 | 0.20 | 0.16 |
| 小车质量m/kg | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
(3)在“探究加速度与力的关系”时,保持小车的质量不变,改变小桶中砝码的质量,该同学根据实验数据作出了加速度a与力F图线如图3所示,该图线不通过坐标原点,试分析图线不通过坐标原点的可能原因是没有平衡摩擦力或平衡摩擦力不足.
 如图所示氢气球受风力作用而使拉住它的细绳与地面的夹角为θ.在细绳被割断的瞬间,气球所受外力的合力为(氢气球的重力忽略不计)( )
如图所示氢气球受风力作用而使拉住它的细绳与地面的夹角为θ.在细绳被割断的瞬间,气球所受外力的合力为(氢气球的重力忽略不计)( )| A. | 与原来绳子的拉力大小相等,方向相反 | |
| B. | 沿风力方向,大小等于风力 | |
| C. | 沿竖直方向向上,大小等于气球所受的浮力 | |
| D. | 与原来绳子的拉力方向相反.大小等于风力与浮力的合力 |
 如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=R2=R3=R4=3.0Ω;电容器的电容C=100μF.求电源的路端电压和电容器所带的电量.
如图所示的电路中,电源的电动势E=3.0V,内阻r=1.0Ω;电阻R1=R2=R3=R4=3.0Ω;电容器的电容C=100μF.求电源的路端电压和电容器所带的电量. 一质量m=2.0kg的小物块在竖直向上的拉力作用下以一定的初速度竖直向上运动(不计阻力),小物块上升过程的速度-时间图线如图所示.(g取10m/s2)求:
一质量m=2.0kg的小物块在竖直向上的拉力作用下以一定的初速度竖直向上运动(不计阻力),小物块上升过程的速度-时间图线如图所示.(g取10m/s2)求: 如图所示,半径R=4m的光滑圆弧轨道BCD与足够长的传送带DE在D处平滑连接,O为圆弧轨道BCD的圆心,C点为圆弧轨道的最低点,半径OB、OD与OC的夹角分别为53°和37°.传送带以2m/s的速度沿顺时针方向匀速转动,将一个质量m=0.5kg的煤块(视为质点)从B点左侧高为h=0.8m处的A点水平抛出,恰从B点沿切线方向进入圆弧轨道.已知煤块与轨道DE间的动摩擦因数μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:
如图所示,半径R=4m的光滑圆弧轨道BCD与足够长的传送带DE在D处平滑连接,O为圆弧轨道BCD的圆心,C点为圆弧轨道的最低点,半径OB、OD与OC的夹角分别为53°和37°.传送带以2m/s的速度沿顺时针方向匀速转动,将一个质量m=0.5kg的煤块(视为质点)从B点左侧高为h=0.8m处的A点水平抛出,恰从B点沿切线方向进入圆弧轨道.已知煤块与轨道DE间的动摩擦因数μ=0.5,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求: