题目内容
用长为L的细绳悬吊着一个小木块, 木块的质量为M, 一颗质量为m的子弹以水平速度v射入木块, 并留在木块中, 和木块一起做圆周运动, 为了保证子弹和小木块一起能在竖直平面内做圆运动, 子弹射入木块的初速度v的大小至少是多少?
解：在子弹射入木块的过程中，子弹和木块组成的系统动量守恒，根据动量守恒定律可得：mv = (M+m)v1所以 v1=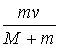
(2分)子弹和木块一起运动后，绳的拉力不做功，只有重力做功。它们从最低点运动到最高点的过程中，根据动能定理有： -（M+m）g×2L = 
- 
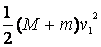(3分) 为了保证子弹和木块一起能在竖直平面内做圆周运动，在最高点它们的速度不能为零。在最高点它们所受的向心力等于重力时速度最小。 （M+m）g=(M+m)
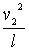(3分)由以上三个方程联立求解可得：v1 =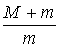 
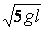即：子弹射入木块的速度至少是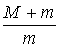 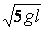（2分）
(2分)子弹和木块一起运动后，绳的拉力不做功，只有重力做功。它们从最低点运动到最高点的过程中，根据动能定理有： -（M+m）g×2L = - (3分) 为了保证子弹和木块一起能在竖直平面内做圆周运动，在最高点它们的速度不能为零。在最高点它们所受的向心力等于重力时速度最小。 （M+m）g=(M+m) (3分)由以上三个方程联立求解可得：v1 = 即：子弹射入木块的速度至少是 （2分） 
练习册系列答案
阅读快车系列答案
相关题目
时（其中μ为工件与皮带之间的动摩擦因素），才有相对静止的过程，否则没有。
= 
（2）
。
。）
= m1
+ m2
+ m3
+ … + mn
只能是系统外力的矢量和，等式右边也是矢量相加。
x 。
Mg ，其中l＜L ，则x＜(L-l)的右段没有张力，x＞(L-l)的左端才有张力。
Mg时（μ为棒与平面的摩擦因素，l为小于L的某一值，M为棒的总质量），当x＜(L-l)，N≡0 ；当x＞(L-l)，N = 
〔x -〈L-l〉〕。
。
= m2a
g
。
= m1
+ m2
+ m3
+ … + mn
，猫和棒的系统外力只有两者的重力，竖直向下，而猫的加速度a1 = 0 ，所以：
g 。
。
求a1 。
。
at2 ②
a1xt2 ③
+ 
* = m 
（注：
*为惯性力），此题极简单。过程如下——
a相 t2 （3）