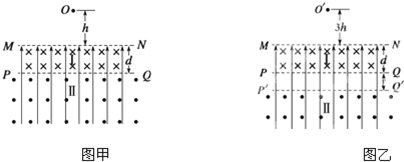Question

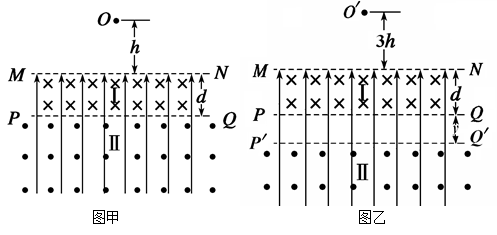
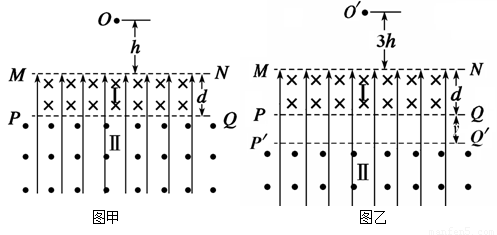
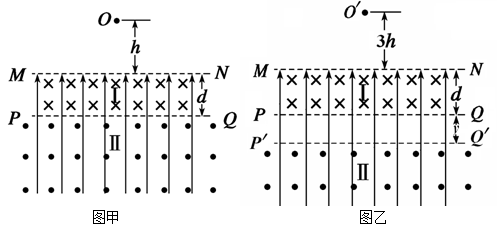
（16分）如图甲所示，空间分布着有理想边界的匀强电场和匀强磁场．匀强磁场分为Ⅰ、Ⅱ两个区域，其边界为MN、PQ，磁感应强度大小均为B，方向如图所示，Ⅰ区域高度为d，Ⅱ区域的高度足够大．一个质量为m、电量为q的带正电的小球从磁场上方的O点由静止开始下落，进入电、磁复合场后，恰能做匀速圆周运动．

(1)求电场强度E的大小；

(2)若带电小球运动一定时间后恰能回到O点，求带电小球释放时距MN的高度h；

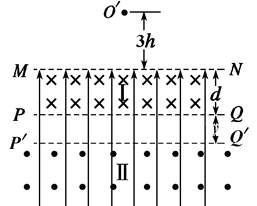
(3)若带电小球从距MN的高度为3h的O'点由静止开始下落，为使带电小球运动一定时间后仍能回到O'点，需将磁场Ⅱ向下移动一定距离（如图乙所示），求磁场Ⅱ向下移动的距离y及小球从O'点释放到第一次回到O'点的运动时间T。

 

Answer 1

解：（1）带电小球进入复合场后恰能做匀速圆周运动，则电场力与重力平衡，得

    mg=qE，解得E=mg/q。     （2分）

（2）只有小球从进入磁场的位置离开磁场，做竖直上抛运动，才能恰好回到O点,

mgh=，qvB=m，

由几何关系得：Rsin60°=d，（4分）

  

解得：   （2分）

（3）当带电小球从距MN的高度为3h的O'点由静止开始下落时，应有，

mg·3h=，qv₁B=m，

R₁=2d。（2分）

      

    画出粒子的运动轨迹，如右图所示，

在中间匀速直线运动过程中，粒子的速度方向与竖直方向成30°角，根据几何关系，可得

y=(6-2)d（2分）

粒子自由落体和竖直上抛的总时间

（1分）

粒子圆周运动的总时间

（1分）

粒子匀速直线运动的总时间

 （1分）

一个来回的总时间

（1分）

 

解析:根据带电粒子在复合场中运动的相关知识列方程解答