��Ŀ����
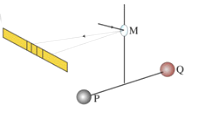
����Ŀ��������̽����2017����ŵ��������ѧ����˫�ǵ��˶��Dz�������������Դ֮һ��������������һ˫��ϵͳ��P��Q����������ɣ������������������ߵ�ijһ���ڶ�����������������������Բ���˶������P�ǵ�����ΪT��P��Q�����ǵľ���Ϊl��P��Q�����ǵĹ���뾶֮��Ϊ��r��P�ǵĹ���뾶����Q�ǵĹ���뾶����������������ΪG��������
A. Q��P�����ǵ�������Ϊ![]()
B. P��Q�����ǵ����ٶȴ�С֮��Ϊ![]()
C. P��Q�����ǵ��˶��뾶֮��Ϊ![]()
D. P��Q�����ǵ�����֮��Ϊ![]()
���𰸡�ABD
��������
A��˫��ϵͳ���������������ṩ�����������ٶȴ�С��ȣ���������С��ȣ����У�![]() mPrP��2��mQrQ��2�����
mPrP��2��mQrQ��2�����![]() ��
��![]() ����Q��P�����ǵ�������Ϊ��m��mQ��mP��
����Q��P�����ǵ�������Ϊ��m��mQ��mP��![]() ����A��ȷ��
����A��ȷ��
B��P��Q�����ǵ����ٶȴ�С֮��Ϊ��v��vP��vQ��![]() ����B��ȷ��
����B��ȷ��
C��˫��ϵͳ���������������ṩ�����������ٶȴ�С��ȣ���������ȣ�����Q�ǵ�����ΪT�����������֪��rP+rQ��l��rP��rQ����r����ã�![]() ��
��![]() ����P��Q�����ǵ��˶��뾶֮��
����P��Q�����ǵ��˶��뾶֮��![]() ��C����
��C����
D��P��Q�����ǵ�����֮��Ϊ![]() ����D��ȷ��
����D��ȷ��

��ϰ��ϵ�д�
 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�
�����Ŀ