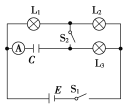
题目内容
【题目】如图所示,平行且足够长的两条光滑金属导轨,相距0.5 m,与水平面夹角均为30°,金属导轨的电阻不计。导轨之间的匀强磁场垂直穿过导轨平面,磁感应强度B=0.4 T。金属棒ab和cd的质量均为0.2 kg,电阻均为0.1 Ω,垂直导轨放置。某时刻棒ab在外力作用下,沿着导轨向上滑动,与此同时,棒cd由静止释放。在运动过程中,棒ab始终保持速度v0=1.5 m/s不变,两金属棒与导轨始终垂直且接触良好。取重力加速度g=10 m/s2。求:
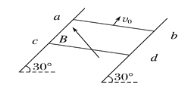
(1)棒ab产生的感应电动势;
(2)闭合回路中的最小电流和最大电流;
(3)棒cd最终稳定运动时的速度大小。
【答案】(1)0.3 V(2)Imin=1.5 A Imax=5 A(3)3.5 m/s
【解析】(1)Eab=BLv0=0.4×0.5×1.5 V=0.3 V
(2)刚释放棒cd时,I1=![]() =1.5 A
=1.5 A
棒cd受到安培力为F1=BI1L=0.4×1.5×0.5 N=0.3 N
棒cd受到的重力沿导轨向下的分力为G1=mgsin 30°=1 N
F1<G1,棒cd沿导轨向下加速运动,即abcd闭合回路的感应电动势增大;电流也增大,所以最小电流为Imin=I1=1.5 A
当棒cd的速度达到最大时,回路的电流最大,此时棒cd的加速度为0
由mgsin 30°=BImaxL
得Imax=![]() =5 A
=5 A
(3)由Imax=![]() 得
得
vcd=3.5 m/s

练习册系列答案
相关题目