题目内容
 如图所示,在倾角θ=30°的斜面上放置一段凹槽B,B与斜面间的动摩擦因数μ=
如图所示,在倾角θ=30°的斜面上放置一段凹槽B,B与斜面间的动摩擦因数μ=
| ||
| 6 |
(1)画出凹槽B运动的速度v随时间t的变化图象;
(2)物块A与凹槽B的左侧壁第n次碰撞后瞬间A、B的速度大小;
(3)从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小.
分析:(1)对B进行受力分析,判断B的运动状态,释放后A做匀加速直线运动,A、B两物体质量相等,发生弹性碰撞时它们交换速度,由牛顿第二定律及运动学公式求出物体的速度,然后画出v-t图象.
(2)由(1)求出A、B碰撞n次后,A、B的速度.
(3)根据A、B的运动过程,应用v-t图象可以求出B的位移.
(2)由(1)求出A、B碰撞n次后,A、B的速度.
(3)根据A、B的运动过程,应用v-t图象可以求出B的位移.
解答:解(1)B与斜面间的滑动摩擦力为:f=μ×2mgcos30°=
mg
B所受重力沿斜面向下的分力为:G1=mgsin30°=
mg
B所受最大静摩擦力等于滑动摩擦力,B沿斜面的分力与最大静摩擦力相等,释放B后,B静止;
释放A后,A做匀加速直线运动,由牛顿第二定律得:mgsin30°=ma,a=5m/s2
由匀变速运动的速度位移公式可得:vA12-0=2ad,A与B碰撞前A的速度为:vA1=1m/s;
A、B碰撞时动量守恒,A、B碰撞时不计机械能损失,碰撞是弹性碰撞,由于A、B质量相等,碰撞时A、B交换速度,碰后A速度为零,B的速度为:vB1=1m/s,碰后B做匀速直线运动,A做初速度为零的匀加速运动,
设经过时间t后,A、B速度相等,vA2=at,t=0.2s,A的位移为:sA1=
at2=0.10m=d,此时间内B沿斜面方向的位移为:SB1=vB1t=0.2m,故此时刻AB的相对位置重新回到初始状态,A相对于B物体的相对运动仍为初速度为零、加速度为a=gsin30°的匀加速直线运动,可知再经过t=0.2s发生第二次碰撞,碰时A球速度为:vA3=vA2+at=0.2+5×0.2m/s=0.3m/s,碰后两球再次交换速度,B的速度改为0.3m/s,A的速度人为0.2m/s,之后重复以上的运动过程,每过0.4s碰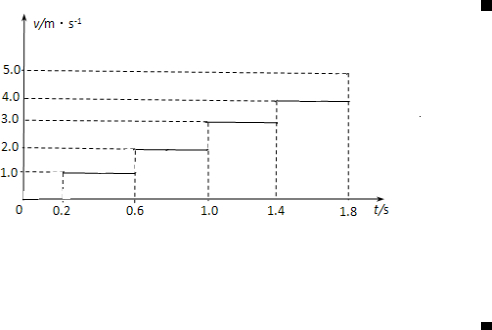 撞一次,碰后B的速度每次增加1m/s,图象如下
撞一次,碰后B的速度每次增加1m/s,图象如下
(2)因为B与斜面间的滑动摩擦力f=μ×2mgcos30°=
mg,B所受重力沿斜面向下的分力G1=mgsin30°=
mg,B所受最大静摩擦力等于滑动摩擦力,B沿斜面的分力与最大静摩擦力相等,释放B后,B静止;
释放A后,A做匀加速直线运动,由牛顿第二定律得:
mgsin30°=ma,
a=5m/s2,
由匀变速运动的速度位移公式可得:vA12-0=2ad,
A与B碰撞前A的速度vA1=1m/s;
A、B碰撞时动量守恒,A、B碰撞时不计机械能损失,碰撞是弹性碰撞,由于A、B质量相等,碰撞时A、B交换速度,碰后A速度为零,B的速度为:
vB1=1m/s,
碰后B做匀速直线运动,A做初速度为零的匀加速运动,设经过时间t后,A、B速度相等,
vA2=at,
t=0.2s,
A的位移sA1=
at2=0.10m=d,
此时间内B沿斜面方向的位移为:
SB1=vB1t=0.2m,
故此时刻AB的相对位置重新回到初始状态,A相对于B物体的相对运动仍为初速度为零、加速度为a=gsin30°的匀加速直线运动,可知再经过t=0.2s发生第二次碰撞,碰时A球速度为:
 vA3=vA2+at=1+5×0.2m/s=2m/s
vA3=vA2+at=1+5×0.2m/s=2m/s
碰后两球再次交换速度,B的速度改为2m/s,A的速度改为1m/s,之后重复以上的运动过程,每过0.4s碰撞一次,碰后B的速度每次增加1m/s
故:vAn=(n-1)m/s,vBn=n m/s
(3)由v--t图象得,从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小为:
x总=0×0.2+1×0.4+2×0.4+---+(n-1)×0.4=0.2n2-0.2n
答:(1)画出凹槽B运动的速度v随时间t的变化图象为:
(2)物块A与凹槽B的左侧壁第n次碰撞后瞬间A、B的速度大小为vAn=(n-1)m/s,vBn=n m/s
(3)从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小为0.2n2-0.2n
| 1 |
| 2 |
B所受重力沿斜面向下的分力为:G1=mgsin30°=
| 1 |
| 2 |
B所受最大静摩擦力等于滑动摩擦力,B沿斜面的分力与最大静摩擦力相等,释放B后,B静止;
释放A后,A做匀加速直线运动,由牛顿第二定律得:mgsin30°=ma,a=5m/s2
由匀变速运动的速度位移公式可得:vA12-0=2ad,A与B碰撞前A的速度为:vA1=1m/s;
A、B碰撞时动量守恒,A、B碰撞时不计机械能损失,碰撞是弹性碰撞,由于A、B质量相等,碰撞时A、B交换速度,碰后A速度为零,B的速度为:vB1=1m/s,碰后B做匀速直线运动,A做初速度为零的匀加速运动,
设经过时间t后,A、B速度相等,vA2=at,t=0.2s,A的位移为:sA1=
| 1 |
| 2 |
 撞一次,碰后B的速度每次增加1m/s,图象如下
撞一次,碰后B的速度每次增加1m/s,图象如下(2)因为B与斜面间的滑动摩擦力f=μ×2mgcos30°=
| 1 |
| 2 |
| 1 |
| 2 |
释放A后,A做匀加速直线运动,由牛顿第二定律得:
mgsin30°=ma,
a=5m/s2,
由匀变速运动的速度位移公式可得:vA12-0=2ad,
A与B碰撞前A的速度vA1=1m/s;
A、B碰撞时动量守恒,A、B碰撞时不计机械能损失,碰撞是弹性碰撞,由于A、B质量相等,碰撞时A、B交换速度,碰后A速度为零,B的速度为:
vB1=1m/s,
碰后B做匀速直线运动,A做初速度为零的匀加速运动,设经过时间t后,A、B速度相等,
vA2=at,
t=0.2s,
A的位移sA1=
| 1 |
| 2 |
此时间内B沿斜面方向的位移为:
SB1=vB1t=0.2m,
故此时刻AB的相对位置重新回到初始状态,A相对于B物体的相对运动仍为初速度为零、加速度为a=gsin30°的匀加速直线运动,可知再经过t=0.2s发生第二次碰撞,碰时A球速度为:
 vA3=vA2+at=1+5×0.2m/s=2m/s
vA3=vA2+at=1+5×0.2m/s=2m/s碰后两球再次交换速度,B的速度改为2m/s,A的速度改为1m/s,之后重复以上的运动过程,每过0.4s碰撞一次,碰后B的速度每次增加1m/s
故:vAn=(n-1)m/s,vBn=n m/s
(3)由v--t图象得,从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小为:
x总=0×0.2+1×0.4+2×0.4+---+(n-1)×0.4=0.2n2-0.2n
答:(1)画出凹槽B运动的速度v随时间t的变化图象为:
(2)物块A与凹槽B的左侧壁第n次碰撞后瞬间A、B的速度大小为vAn=(n-1)m/s,vBn=n m/s
(3)从初始位置到物块A与凹槽B的左侧壁发生第n次碰撞时B的位移大小为0.2n2-0.2n
点评:本题是复杂的力学综合题,分析运动情况,把握每个过程的物理规律是关键.对于A、B的碰撞过程,属于弹性碰撞过程,两者质量相等,交换速度.此外注意应用图象求解位移是个好方法

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2011?安徽模拟)如图所示,在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB.平板的上表面光滑,其下端B与斜面底端C的距离为7m.在平板的上端A处放一质量m=0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放.设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5,求滑块与平板下端B到达斜面底端C的时间差△t.(sin37°=0.6,cos37°=0.8,g=10m/s2)
(2011?安徽模拟)如图所示,在倾角θ=37°的固定斜面上放置一质量M=1kg、长度L=3m的薄平板AB.平板的上表面光滑,其下端B与斜面底端C的距离为7m.在平板的上端A处放一质量m=0.6kg的滑块,开始时使平板和滑块都静止,之后将它们无初速释放.设平板与斜面间、滑块与斜面间的动摩擦因数均为μ=0.5,求滑块与平板下端B到达斜面底端C的时间差△t.(sin37°=0.6,cos37°=0.8,g=10m/s2) (2010?南昌一模)如图所示,在倾角为a的传送带上有质量均为m的三个木块1、2,3,中间均用原长为L,劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运行,三个木块处于平衡状态.下列结论正确的是( )
(2010?南昌一模)如图所示,在倾角为a的传送带上有质量均为m的三个木块1、2,3,中间均用原长为L,劲度系数为k的轻弹簧连接起来,木块与传送带间的动摩擦因数均为μ,其中木块1被与传送带平行的细线拉住,传送带按图示方向匀速运行,三个木块处于平衡状态.下列结论正确的是( ) 如图所示,在倾角θ=37°的斜面上,固定着宽L=0.20m的平行金属导轨,在导轨上端接有电源和滑动变阻器,已知电源电动势E=6.0V,内电阻r=0.50Ω.一根质量m=10g的金属棒ab放在导轨上,与两导轨垂直并接触良好,导轨和金属棒的电阻忽略不计.整个装置处于磁感应强度B=0.50T、垂直于轨道平面向上的匀强磁场中.若金属导轨是光滑的,已知sin37°=0.6,cos37°=0.8,取g=10m/s2,求:
如图所示,在倾角θ=37°的斜面上,固定着宽L=0.20m的平行金属导轨,在导轨上端接有电源和滑动变阻器,已知电源电动势E=6.0V,内电阻r=0.50Ω.一根质量m=10g的金属棒ab放在导轨上,与两导轨垂直并接触良好,导轨和金属棒的电阻忽略不计.整个装置处于磁感应强度B=0.50T、垂直于轨道平面向上的匀强磁场中.若金属导轨是光滑的,已知sin37°=0.6,cos37°=0.8,取g=10m/s2,求: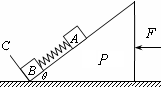 如图所示,在倾角为θ的光滑斜劈P的斜面上有两个用轻质弹簧相连的物块A、B,C为一垂直固定在斜面上的挡板.A、B质量均为m,斜面连同挡板的质量为M,弹簧的劲度系数为k,系统静止于光滑水平面.现开始用一水平恒力F作用于P,(重力加速度为g)下列说法中正确的是( )
如图所示,在倾角为θ的光滑斜劈P的斜面上有两个用轻质弹簧相连的物块A、B,C为一垂直固定在斜面上的挡板.A、B质量均为m,斜面连同挡板的质量为M,弹簧的劲度系数为k,系统静止于光滑水平面.现开始用一水平恒力F作用于P,(重力加速度为g)下列说法中正确的是( ) 如图所示,在倾角α=37°的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一质量m=3kg,中间有一圈凹槽的圆柱体,并用与斜面夹角β=37°的力F拉住,使整个装置处于静止状态.不计一切摩擦,求拉力F和斜面对圆柱体的弹力N的大小. (g=10m/s2,sin37°=0.6,cos37°=0.8)
如图所示,在倾角α=37°的斜面上,一条质量不计的皮带一端固定在斜面上端,另一端绕过一质量m=3kg,中间有一圈凹槽的圆柱体,并用与斜面夹角β=37°的力F拉住,使整个装置处于静止状态.不计一切摩擦,求拉力F和斜面对圆柱体的弹力N的大小. (g=10m/s2,sin37°=0.6,cos37°=0.8)