题目内容
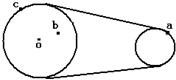如图所示，为一皮带传动装置，右轮的半径为r，a是它的边缘上的一点，左轮的半径为2r，b点距左轮中心距离为r，c点位于左轮边缘上，若在传动过程中，皮带不打滑，则（ ）| A、a点与b点线速度大小相等 | B、a点与c点角速度大小相等 | C、b点与c点角速度大小相等 | D、a、b、c三点，加速度最小的是b点 |
分析：靠传送带传到的各点线速度大小相等，共轴转动的角速度相等，根据v=rω、a=
=rω2比较各点的线速度、角速度、加速度大小关系．
| v2 |
| r |
解答：解：A、a、c两点靠传送带传到，则a、c的线速度大小相等，b、c共轴转动，角速度相等，c的半径是b的半径的2倍，则c的线速度是b的线速度的2倍，所以a的线速度是b的线速度的2倍．c的半径是a的半径的2倍，根据v=rω，知a的角速度是c的角速度的2倍．故A、B错误，C正确．
D、a、c的线速度大小相等，根据a=
知，a的加速度是c的2倍，b、c的角速度相等，
根据a=rω2知，c的加速度是b的加速度的2倍，可知b的加速度最小．故D正确．
故选：CD．
D、a、c的线速度大小相等，根据a=
| v2 |
| r |
根据a=rω2知，c的加速度是b的加速度的2倍，可知b的加速度最小．故D正确．
故选：CD．
点评：解决本题的关键知道靠传送带传到轮子边缘上点的线速度大小相等，共轴转动的各点角速度大小相等．
练习册系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
如图所示，工厂利用皮带传输机把货物从地面运送到高出水平地面的C平台上，C平台离地面的高度一定．运输机的皮带以一定的速度v顺时针转动且不打滑．将货物轻轻地放在A处，货物随皮带到达平台．货物在皮带上相对滑动时，会留下一定长度的痕迹．已知所有货物与皮带间的动摩擦因数为μ．若皮带的倾角θ、运行速度v和货物质量m都可以改变，始终满足tanθ＜μ．可以认为最大静摩擦力等于滑动摩擦力（ ）
，依次将相同货物以相同方式无初速地放到A处，则每一货物的质量不超过多少？
，依次将相同货物以相同方式无初速地放到A处，则每一货物的质量不超过多少？