题目内容
20.足够长的光滑水平面离地面高度h=0.45m,质量均为m=1kg的物块A与长木板B叠放在一起,以v0=4m/s的速度与物块C发生弹性碰撞,取水平向右为正方向,碰撞后瞬间B板速度v1=-2m/s,长木板B的J边未进入PQ区域时,与物块A已到共速,已知A、B间动摩擦因数μ=0.1,g取10m/s2,当B板的J边处在宽d=1m的PQ区域内时,B板就会受到一个水平向左的恒力F,使B板最终向左离开该区域,且A始终没有滑落B板.求:
(1)B板右端J边刚进入边界P的速度v2;
(2)物块C离开水平面做平抛运动的水平位移s;
(3)讨论:F在不同的可能取值范围,B板右端J边处在PQ区域的时间t与恒力F的关系.如果F=5N,计算B板最终的速度v.
分析 (1)由动量守恒定律可以求出物体速度.
(2)由动量守恒定律、机械能守恒定律与平抛运动可以求出物体的水平位移.
(3)由匀变速运动的速度位移公式与牛顿第二定律分析答题.
解答 解:(1)B、C碰后,以A、B为系统,直到共速过程系统动量守恒,
以向右为正方向,由动量守恒定律得:mv0+mv1=2mv2,
解得,J边进入PQ区域的速度:v2=1m/s;
(2)B、C发生弹性碰撞,设C质量为mc,碰后速度为vc,
以向右为正方向,由动量守恒定律得:mv0=mv1+mCvC,
由机械能守恒定律得:$\frac{1}{2}$mv02=$\frac{1}{2}$mv12+$\frac{1}{2}$mCvC2,
代入数据解得:v1=-2m/s,mC=3kg,vC=2m/s,
C离开水平面后做平抛运动,
竖直方向:h=$\frac{1}{2}$gt2,水平方向:s=vCt,代入数据解得:s=0.6m;
(3)设J边进入PQ区域,刚好能到达Q边界:vt=0,
由匀变速直线运动的速度位移公式得:vt2-v22=2(-a)d,
代入数据解得:a=0.5 m/s2,
由牛顿第二定律得,恒力:F1=2ma=2×1×0.5=1N,
设J边进入PQ区域,A、B恰好能一起做匀变速运动,
A有最大加速度am=μg=0.1×10=1m/s2,
恒力:F2=2mam=2×1×1=2N,
讨论:当1 N<F≤2N时,A、B一起匀变速运动,加速度:a1=$\frac{F}{2m}$,
进入及返回的过程互逆,所以:t1=$\frac{2{v}_{1}}{{a}_{1}}$=$\frac{4}{F}$;
当F>2N时,A、B发生相对滑动,B的加速度:a2=$\frac{F-μmg}{m}$,
进入及返回的过程互逆,所以:t2=$\frac{2{v}_{1}}{{a}_{2}}$=$\frac{2}{F-1}$;
F=5N,t=0.5s,B板右端J边离开P,此时A的速度:vA=v2-amt=0.5m/s,
以A的初速度方向为正方向,A、B系统动量守恒,
由动量守恒定律得:m(-v2)+mvA=2mv,
代入数据解得:v=-0.25m/s,方向:水平向左;
答:(1)B板右端J边刚进入边界P的速度v2=1m/s;
(2)物块C离开水平面做平抛运动的水平位移为0.6m;
(3)当1N<F≤2N时,t1=$\frac{4}{F}$,当F>2N时,t2=$\frac{2}{F-1}$,当F=5N时,v=0.25m/s,方向向左.
点评 本题是一道力学综合题,是多体多过程问题,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律、机械能守恒定律与牛顿第二定律即可正确解题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案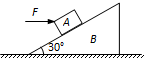 如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )
如图所示,质量为m的物体A静止在倾角为θ=30°、质量为M的斜面体B上.现用水平力F推物体A,在F由零增大至$\frac{\sqrt{3}mg}{2}$再逐渐减为零的过程中,A和B始终保持静止.对此过程下列说法正确的是( )| A. | 地面对B的支持力大于(M+m)g | |
| B. | A对B的压力的最小值为$\frac{\sqrt{3}mg}{2}$,最大值为$\frac{3\sqrt{3}mg}{4}$ | |
| C. | A受到摩擦力的最小值为0,最大值为$\frac{mg}{4}$ | |
| D. | A受到摩擦力的最小值为$\frac{mg}{2}$,最大值为$\frac{3mg}{4}$ |

| A. | 甲图是卡文迪许测定引力常量的实验 | |
| B. | 乙图中玻璃管抽成真空后,重的物体比轻的物体下落的快 | |
| C. | 丙图中砝码所受到的重力等于小车的合外力 | |
| D. | 丁图是伽利略说明“力不是维持物体运动状态的原因”所用的实验装置 |
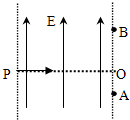 如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )
如图所示,不计重力的两个质量相同的带电粒子,以相同的速度从P点水平射入一个有边界、方向竖直向上的匀强电场中,分别从A点和B点离开电场,且AO<BO,下列判断正确的是( )| A. | 两个粒子电性相反 | |
| B. | 两个粒子在电场中运动的时间不一样 | |
| C. | 两个粒子做匀速圆周运动 | |
| D. | 两个粒子的电势能均减小 |
| A. | α粒子散射实验揭示了原子核内部的复杂性 | |
| B. | 光电效应实验揭示了光的粒子性 | |
| C. | 基态氢原子吸收一个光子跃迁到激发态后,可能发射多种频率的光子 | |
| D. | Th核发生一次α衰变时,新核与原来的原子核相比,中子数减少了4 |
 如图所示,1、2、3、4表示某电场的一组等势线,曲线abc表示某带电粒子只受电场力作用时在电场中的运动轨迹,其运动轨迹与等势面4相切于b点,下列说法正确的是( )
如图所示,1、2、3、4表示某电场的一组等势线,曲线abc表示某带电粒子只受电场力作用时在电场中的运动轨迹,其运动轨迹与等势面4相切于b点,下列说法正确的是( )| A. | 粒子可能带正电,也可能带负电 | |
| B. | 粒子运动至b点时一定是电势能最小 | |
| C. | 不论粒子是从a运动至c或从c运动至a,粒子运动的加速度总是先增大后减小 | |
| D. | 粒子运动至b点时电场力做功瞬时功率为零 |


 如图所示,粗糙水平轨道AB与处于竖直平面内的四分之一圆弧形粗糙轨道BC相切于B点且平滑连接.圆弧的半径R=0.40m,有一质量m=0.20k的物块(可视为质点)放在水平轨道上与B端距离s=0.8m的位置,在一斜向右上与水平方向成37°恒力F=2N的作用下由静止开始运动,当物块运动到圆弧形轨道的C端时,速度恰好为零.物块与水平面的动摩擦因数μ=0.4,取g=10m/s2,求:
如图所示,粗糙水平轨道AB与处于竖直平面内的四分之一圆弧形粗糙轨道BC相切于B点且平滑连接.圆弧的半径R=0.40m,有一质量m=0.20k的物块(可视为质点)放在水平轨道上与B端距离s=0.8m的位置,在一斜向右上与水平方向成37°恒力F=2N的作用下由静止开始运动,当物块运动到圆弧形轨道的C端时,速度恰好为零.物块与水平面的动摩擦因数μ=0.4,取g=10m/s2,求: