题目内容
如图所示,两块带有等量异种电荷的平行金属板分别固定在绝缘板的两端,组成一带电框架,两平行金属板间的距离L=1 m,框架右端带负电的金属板上固定一根原长lo=0.5 m的绝缘轻弹簧,框架的总质量M=9 kg,由于带电,两金属板间产生了高电压U=2×103 V,现用一质量m=1 kg,带电量q=+5×10-2 C的带电小球将弹簧压缩△l=0.2 m后用细线拴住,致使弹簧具有EP=65 J的弹性势能,现使整个装置在光滑水平面上以V0=1 m/s的速度向右运动,运动中拴小球的细线突然断裂致使小球被弹簧弹开,不计一切摩擦,且电势能的变化量等于电场力和相对于电场方向位移的乘积.问:
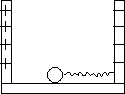
(1)当小球刚好被弹簧弹开时,小球与框架的速度分别为多大?
(2)在细线断裂以后的运动中,小球能否与左端金属板发生碰撞?
解析:
|
(1)当弹簧刚好恢复原长时小球与弹簧分离,设此时小球的速度为v1,框架的速度为v2,根据动量守恒:mv1+Mv2=(m+M)v0 (2分) 根据能量守恒: 代入数值后解得:v1=-8/s v2=2 m/s (2分); (2)当小球与框架速度相等时,小球相对框架的位移最大,根据动量守恒,此时两者的共同速度仍为v0 (2分) 设从小球被弹开至两者速度再次相等小球对地的位移为s1,框架对地的位移为s2,根据动能定理有 代入数值解得s1=31.5 cm s2=13.5 cm (2分) 因s1+s2=0.45 m<0.5 m,故小球不会碰到左侧金属板. (1分) |

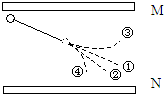 如图所示,带有等量异种电荷的两块等大平行金属板M、N水平正对放置,两板间有一带电粒子以速度v0沿直线运动,当微粒运动到P点时,将M板迅速上移一小段距离,则此后微粒的可能运动情况是( )
如图所示,带有等量异种电荷的两块等大平行金属板M、N水平正对放置,两板间有一带电粒子以速度v0沿直线运动,当微粒运动到P点时,将M板迅速上移一小段距离,则此后微粒的可能运动情况是( )
 A.沿轨迹④运动 B.沿轨迹①运动
A.沿轨迹④运动 B.沿轨迹①运动
 A.沿轨迹④运动 B.沿轨迹①运动
A.沿轨迹④运动 B.沿轨迹①运动