题目内容
(8分) 如图:直杆上O1O2两点间距为L,细线O1A长为 L,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度
L,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度 转动.
转动.

 L,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度
L,O2A长为L,A端小球质量为m,要使两根细线均被拉直,杆应以多大的角速度 转动.
转动. 
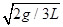
 <
< <
<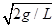
当 较小时,线O1A拉直,O2A松弛;当
较小时,线O1A拉直,O2A松弛;当 较大时,线O2A拉直,O1A松弛。设O2A刚好拉直,但FO2A又为零时,角速度为
较大时,线O2A拉直,O1A松弛。设O2A刚好拉直,但FO2A又为零时,角速度为 1,此时
1,此时 O2O1A=300,对小球:
O2O1A=300,对小球:
FO1A
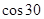 0=mg ①
0=mg ①
FO1A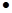
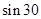 0=m
0=m 12
12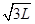
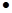
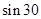 0
0  ② (2分)
② (2分)
由①②解得 1=
1=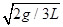 (1分)
(1分)
设O1A由拉紧转到刚被拉直,FO2A变为零时,角速度为 2,对小球:
2,对小球:
FO2A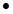
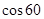 0=mg
0=mg
FO2A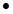
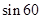 0=m
0=m 22L
22L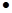
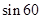 0 (2分)
0 (2分)
解得 2=
2=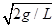 (1分)
(1分)
故杆转动的角速度范围为: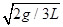
 <
< <
<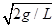 (2分)
(2分)
本题考查匀速圆周运动的临界问题,当角速度较小时,只有OA段绳子由拉力,设当角速度为w1时绳子O2A伸直但没有拉力,此时由O1A和重力的合力提供向心力,分析受力情况可知绳子在竖直方向的分力与重力平衡,水平方向的分力提供向心力,由角度可求得向心力的大小,再由F=mw2r可求得加速度大小,同理当角速度较大时绳子O1A上有拉力,列公式可求得最大角速度,在这两个值之间取值即可
 较小时,线O1A拉直,O2A松弛;当
较小时,线O1A拉直,O2A松弛;当 较大时,线O2A拉直,O1A松弛。设O2A刚好拉直,但FO2A又为零时,角速度为
较大时,线O2A拉直,O1A松弛。设O2A刚好拉直,但FO2A又为零时,角速度为 1,此时
1,此时 O2O1A=300,对小球:
O2O1A=300,对小球:FO1A
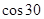 0=mg ①
0=mg ①FO1A
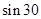 0=m
0=m 12
12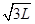
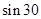 0
0  ② (2分)
② (2分) 由①②解得
 1=
1=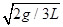 (1分)
(1分)设O1A由拉紧转到刚被拉直,FO2A变为零时,角速度为
 2,对小球:
2,对小球:FO2A
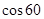 0=mg
0=mgFO2A
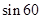 0=m
0=m 22L
22L
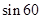 0 (2分)
0 (2分)解得
 2=
2=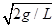 (1分)
(1分)故杆转动的角速度范围为:
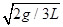
 <
< <
<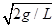 (2分)
(2分)本题考查匀速圆周运动的临界问题,当角速度较小时,只有OA段绳子由拉力,设当角速度为w1时绳子O2A伸直但没有拉力,此时由O1A和重力的合力提供向心力,分析受力情况可知绳子在竖直方向的分力与重力平衡,水平方向的分力提供向心力,由角度可求得向心力的大小,再由F=mw2r可求得加速度大小,同理当角速度较大时绳子O1A上有拉力,列公式可求得最大角速度,在这两个值之间取值即可

练习册系列答案
相关题目









