题目内容
倾角为37°的斜面固定在水平面上，质量m=2.0kg的小物块受到沿斜面向上的F=20.0N的拉力作用，小物块由静止沿斜面向上运动．小物块与斜面间的动摩擦因数μ=0.25（斜面足够长，取g=l0m/s2．sin37°=0.6，cos37°=0.8）
（1）求小物块运动过程中所受摩擦力的大小；
（2）求在拉力的作用过程中，小物块加速度的大小；
（3）求小物块沿斜面向上运动0.25m时的速度．
（1）求小物块运动过程中所受摩擦力的大小；
（2）求在拉力的作用过程中，小物块加速度的大小；
（3）求小物块沿斜面向上运动0.25m时的速度．
分析：对物体进行受力分析，利用正交分解和牛顿第二定律列出等式，求出未知的力和加速度，在结合运动学公式求解运动距离．
解答：解；（1）选物体为研究对象，对其受力分析如下图，将G进行分解，由题意知，
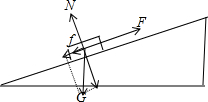支持力为：N=Gcos37°…①
摩擦力为：f=μN…②
由①②解得：f=μGcos37°=4N…③
（2）沿斜面方向的合力：
F合=F-f-Gsin37°…④
由牛顿第二定律得，物体加速度为：
a=
…⑤
由③④⑤得，a=2m/s2…⑥
（3）物块沿斜面做匀加速直线运动，由运动学公式知，
v2=2ax…⑦
∴v=
=1m/s…⑧
答（1）小物块运动过程中所受摩擦力的大小为4N
（2）在拉力的作用过程中，小物块加速度的大小为2m/s2
（3）小物块沿斜面向上运动0.25m时的速度为1m/s
支持力为：N=Gcos37°…①摩擦力为：f=μN…②
由①②解得：f=μGcos37°=4N…③
（2）沿斜面方向的合力：
F合=F-f-Gsin37°…④
由牛顿第二定律得，物体加速度为：
a=
| F合 |
| m |
由③④⑤得，a=2m/s2…⑥
（3）物块沿斜面做匀加速直线运动，由运动学公式知，
v2=2ax…⑦
∴v=
| 2ax |
答（1）小物块运动过程中所受摩擦力的大小为4N
（2）在拉力的作用过程中，小物块加速度的大小为2m/s2
（3）小物块沿斜面向上运动0.25m时的速度为1m/s
点评：解题的关键是能正确对物体进行受力分析，并能对力进行正交分解，运用牛顿第二定律列出等式求出问题，还能结合运动学公式去求．
练习册系列答案
快乐5加2金卷系列答案
相关题目
（2010?闵行区三模）如图所示，一倾角为37°的斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达C点时速度为零．每隔0.2s通过速度传感器测得物体的瞬时速度，下表给出了部分测量数据．（取 sin37°=0.6．cos37°=0.8）试求：
（2011?普陀区二模）如图所示，一倾角为37°的斜面固定在水平地面上，质量为1千克的物体在平行于斜面向上的恒力F作用下，从斜面的底端A点由静止开始运动，到达B点时立即撤去拉力F．此后，物体到达最高点C．每隔0.2s通过位移传感器测得物体的瞬时速度的大小，下表给出了部分测量数据．（取sin37°=0.6，cos37°=0.8）
（2012?石家庄一模）如图所示，倾角为37°的斜面固定在水平地面上，质量m=1kg的物体在平行于斜面向上的恒力F作用下，从A点由静止开始运动，到达B点时立即撤去拉力F，此后，物体到达C点时速度为零．通过速度传感器测得这一过程中物体每隔0.2s的瞬时速度，下表给出了部分数据．求：
如图所示，倾角为θ=37°的斜面固定在水平桌面上，劲度系数为200N/m的轻质弹簧上端固定在斜面顶端的木板上，下端连接孩子两位1kg的物块A，弹簧与斜面平行；物块A的下面用跨过光滑定滑轮的轻绳连接质量为0.15kg的物块B，物块A与滑轮之间的轻绳平行于斜面；B的下面用轻绳连接质量为0.95kg的物块C．此时弹簧的伸长量为6cm，整个装置处于静止状态．取g=10m/s2，sin37°=0.6．则下列说法中正确的是（ ）| A、物块A受到6个作用力 | B、物块A受到的摩擦力方向沿斜面向上，大小为5N | C、剪断B、C间轻绳后，物块A收到的摩擦力方向沿斜面向下 | D、剪断A、B间轻绳后，物块A一定沿斜面向上运动 |