题目内容
8.如图甲所示,在y轴右侧加有垂直纸面向外的匀强磁场,磁感应强度B=1T.从原点O处向第Ⅰ象限发射一比荷$\frac{q}{m}$=1×104C/kg的带正电的粒子(重力不计),速度大小v0=103m/s,方向垂直于磁场且与x轴正方向成30°角.
(1)求粒子在该匀强磁场中做匀速圆周运动的半径R和在该磁场中运动的时间t1.
(2)若磁场随时间变化的规律如图乙所示(垂直于纸面向外为正方向),t=$\frac{4π}{3}$×10-4s后空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度v0射入,求粒子从O点射出后第2次经过x轴时的坐标.
分析 (1)由洛伦兹力提供向心力列方程求运动半径,根据公式t=$\frac{θ}{2π}•\frac{2πm}{Bq}$求运动时间.
(2)后面不存在磁场则粒子做匀速直线运动,画出轨迹结合几何知识求再次经过x轴的坐标.
解答 
 解:(1)轨迹如图甲所示.由$Bqv=m\frac{{v}^{2}}{R}$得
解:(1)轨迹如图甲所示.由$Bqv=m\frac{{v}^{2}}{R}$得
轨迹半径$R=\frac{mv}{Bq}$=$\frac{1{0}^{3}}{1×1{0}^{4}×1}$=0.1m,
粒子运动周期T=$\frac{2πm}{Bq}$=$\frac{2π}{1×1{0}^{4}×1}$=2π×10-4s
粒子在磁场中轨迹所对的圆心角为240°,
所以粒子在磁场中运动的时间为t1=$\frac{2T}{3}=\frac{4π}{3}×1{0}^{-4}s$
(2)磁场变化的半周期为$△t=\frac{2π}{3}×1{0}^{-4}s=\frac{T}{3}$
在图乙中,∠OO1C=∠CO2D=120°,且O1O2平行于x轴
OE=2(R+Rsin30°)=3R=0.3m
Rt△EDP中,∠EDP=60°,DE=2Rsin60°
EP=DEtan60°=3R=0.3m
则粒子从O点射出后第2次经过x轴时的坐标xp=OE+EP=0.6m
答:(1)求粒子在该匀强磁场中做匀速圆周运动的半径R未0.1m,在该磁场中运动的时间t1为$\frac{4π}{3}×1{0}^{-4}s$.
(2)若磁场随时间变化的规律如图乙所示(垂直于纸面向外为正方向),t=$\frac{4π}{3}$×10-4s后空间不存在磁场.在t=0时刻,粒子仍从O点以与原来相同的速度ν0射入,粒子从O点射出后第2次经过x轴时的坐标为0.6m.
点评 该题考查带电粒子在匀强磁场中的运动,洛伦兹力提供向心力是基础,正确画出粒子运动的轨迹是解决问题的关键.

 如图所示,处于真空中的匀强电场与水平方向成15°角,直线AB与匀强电场E互相垂直.在A点以大小为v0的初速度水平抛出一质量为m,带电量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时速度仍为v0,在小球由A点运动到C点的过程中,下列说法中正确的是( )
如图所示,处于真空中的匀强电场与水平方向成15°角,直线AB与匀强电场E互相垂直.在A点以大小为v0的初速度水平抛出一质量为m,带电量为+q的小球,经时间t,小球下落一段距离过C点(图中未画出)时速度仍为v0,在小球由A点运动到C点的过程中,下列说法中正确的是( )| A. | 电场力对小球做功为零 | |
| B. | 小球的电势能增加 | |
| C. | 小球的机械能减少量一定大于$\frac{1}{2}$mg2t2 | |
| D. | C可能位于AB直线的左侧 |

| A. | 前2s内物体做匀速直线运动 | B. | 1s末物体运动方向发生改变 | ||
| C. | 第3s内和第4s内物体速度方向相反 | D. | 第2s末物体运动方向发生改变 |
 如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻不计的金属棒从轨道最低位置cd开始,在拉力作用下以速度υ0向右沿轨道做匀速圆周运动至ab处,则该过程中( )
如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、电阻不计的金属棒从轨道最低位置cd开始,在拉力作用下以速度υ0向右沿轨道做匀速圆周运动至ab处,则该过程中( )| A. | 通过R的电流方向为由内向外 | B. | 通过R的电流方向为由外向内 | ||
| C. | R上产生的热量为$\frac{{π{B^2}{L^2}r{υ_0}}}{4R}$ | D. | 流过R的电量为$\frac{BLr}{R}$ |
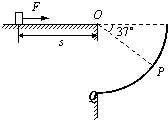 如图所示,在粗糙水平台阶上放置一质量m=0.5kg的小物块,它与水平台阶间的动摩擦因数μ=0.5,与台阶边缘O点的距离s=5m.在台阶右侧固定一个$\frac{1}{4}$光滑圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力F,小物块最终水平抛出并击中挡板.(已知:sin37°=0.6,cos37°=0.8,取g=10m/s2)
如图所示,在粗糙水平台阶上放置一质量m=0.5kg的小物块,它与水平台阶间的动摩擦因数μ=0.5,与台阶边缘O点的距离s=5m.在台阶右侧固定一个$\frac{1}{4}$光滑圆弧挡板,圆弧半径R=1m,圆弧的圆心也在O点.现用F=5N的水平恒力拉动小物块,一段时间后撤去拉力F,小物块最终水平抛出并击中挡板.(已知:sin37°=0.6,cos37°=0.8,取g=10m/s2) 一根长为L的丝线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成60°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求:
一根长为L的丝线吊着一质量为m的带电量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成60°角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响,(重力加速度为g),求: 如图所示,质量为M=55kg的人,用绳子通过滑轮拉住一个质量为m=10kg的物体保持静止,绳与竖直方向的夹角θ=60°,已知人与地面间的动摩擦因数μ=0.6,g取10N/kg,求:
如图所示,质量为M=55kg的人,用绳子通过滑轮拉住一个质量为m=10kg的物体保持静止,绳与竖直方向的夹角θ=60°,已知人与地面间的动摩擦因数μ=0.6,g取10N/kg,求: