题目内容
2.一个做匀加速直线运动的物体,通过A点的瞬时速度是v1,通过B点的瞬时速度是v2,那么它通过AB时间正中间时刻的瞬时速度为$\frac{{v}_{1}+{v}_{2}}{2}$,它通过AB位移正中间位置的瞬时速度为$\sqrt{\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{2}}$.分析 根据匀变速直线运动的平均速度推论求出中间时刻的瞬时速度,根据匀变速直线运动的速度位移公式求出通过中间位置的速度.
解答 解:根据匀变速直线运动平均速度推论知,某段时间内的平均速度等于中间时刻的瞬时速度,则有:
${v}_{\frac{t}{2}}=\frac{{v}_{1}+{v}_{2}}{2}$.
设中间位置的速度为${v}_{\frac{x}{2}}$,根据速度位移公式有:
${{v}_{\frac{x}{2}}}^{2}-{{v}_{1}}^{2}=2a\frac{x}{2}$,${{v}_{2}}^{2}-{{v}_{\frac{x}{2}}}^{2}=2a\frac{x}{2}$,
解得:${v}_{\frac{x}{2}}=\sqrt{\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{2}}$.
故答案为:$\frac{{v}_{1}+{v}_{2}}{2}$,$\sqrt{\frac{{{v}_{1}}^{2}+{{v}_{2}}^{2}}{2}}$.
点评 解决本题的关键掌握匀变速直线运动的运动学公式和推论,并能灵活运用,基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
17.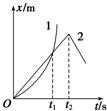 如图所示的x-t图象中,给出的两条图线线1、2,分别代表甲、乙两个不同物体位移随时间变化的图象,关于它们的物理意义,下列描述正确的是( )
如图所示的x-t图象中,给出的两条图线线1、2,分别代表甲、乙两个不同物体位移随时间变化的图象,关于它们的物理意义,下列描述正确的是( )
 如图所示的x-t图象中,给出的两条图线线1、2,分别代表甲、乙两个不同物体位移随时间变化的图象,关于它们的物理意义,下列描述正确的是( )
如图所示的x-t图象中,给出的两条图线线1、2,分别代表甲、乙两个不同物体位移随时间变化的图象,关于它们的物理意义,下列描述正确的是( )| A. | 曲线1表示物体甲做曲线运动 | |
| B. | 由图象可知中,t1时刻甲、乙两个物体的速度v1=v2 | |
| C. | 图象中0至t1时间内物体乙的平均速度比甲的平均速度大 | |
| D. | 图象中t2时刻表示物体乙开始反向运动 |
7.变轨技术在飞船和空间站对接过程中有着广泛的应用.若某空间站运动的轨道可近似看做是以地心为中心,半径为r1的圆,现有一艘准备和该空间站对接的飞船已被火箭送入较为接近空间站的轨道,它正以地心为中心,半径为r2做匀速圆周运动.已知r1>r2,现开动飞船上的小火箭,以实现飞船和空间站成功对接,下列说法正确的有( )
| A. | 小火箭应向飞船前进的方向喷出燃气 | |
| B. | 小火箭应向飞船前进的后方喷出燃气 | |
| C. | 当飞船和空间站对接成功后,飞船的速度变小 | |
| D. | 当飞船和空间站对接成功后,飞船的速度增大 |
16.下列说法正确的是( )
| A. | 力是维持物体运动的原因 | |
| B. | 作用力和反作用力可以是不同性质的力 | |
| C. | 静摩擦力的方向可以与速度方向共线或成一夹角 | |
| D. | 牛顿第一定律可以通过实验进行验证 |
 在“探究导体电阻与材料的关系”的实验中,一同学先用刻度尺测出金属丝的长度l=10.05cm,用螺旋测微器测m金属丝的直径d.
在“探究导体电阻与材料的关系”的实验中,一同学先用刻度尺测出金属丝的长度l=10.05cm,用螺旋测微器测m金属丝的直径d. 一个滑块沿斜面由静止滑下做匀变速直线运动,依次通过斜面上的A、B、C三点,如图所示,已知AB=10m,BC=20m,滑块经过AB、BC两段位移的时间都是2s,求
一个滑块沿斜面由静止滑下做匀变速直线运动,依次通过斜面上的A、B、C三点,如图所示,已知AB=10m,BC=20m,滑块经过AB、BC两段位移的时间都是2s,求 某同学用如图甲所示的装置研究合力与分力之间是否遵从平行四边形定则,实验步骤如下:
某同学用如图甲所示的装置研究合力与分力之间是否遵从平行四边形定则,实验步骤如下: 一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时开始沿x轴正向运动.求:
一质点沿x轴做直线运动,其v-t图象如图所示.质点在t=0时开始沿x轴正向运动.求: