题目内容
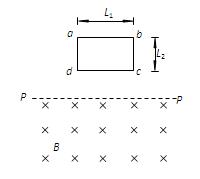
如图所示，矩形单匝导线框abcd竖直放置，其下方有一磁感应强度为B的匀强磁场区域，该区域的上边界水平，并与线框的ad边平行，磁场方向与线框平面垂直．已知线框ab边长为h，ad边长为L，线框质量为m，总电阻为R．现无初速地释放线框，在下落过程中线框所在平面始终与磁场垂直，且线框的ad边始终保持水平．重力加速度为g．若线框恰好匀速进入磁场，则下列结论正确的是（ ）分析：线框匀速进入磁场，重力与安培力平衡．安培力与速度成正比，根据安培力经验公式 F=
，由安培力可求出速度．根据能量守恒求解焦耳热．
由动能定理和功的计算公式，求出重力做的功W．
| B2L2v |
| R |
由动能定理和功的计算公式，求出重力做的功W．
解答：解：A、由于线框匀速进入磁场，则根据平衡条件知，线框进入磁场时受安培力的大小F=mg．故A正确．
B、线框bc边刚进入磁场时，感应电动势 E=BLv，感应电流 I=
，得bc边受安培力的大小 F=BIL=
；
又 F=mg
解得，线框速度的大小 v=
，故B正确．
C、D、在线框从开始下落到bc边刚进入磁场的过程中，重力做功W1，根据动能定理得：
W1=
mv2=
m(
)2=
在线框从bc边刚进入磁场到ad边刚进入磁场的过程中，重力做功W2．
W2=mgh
所以在线框从开始下落到ad边刚进入磁场的过程中，重力做功：W=W1+W2=
+mgh．
根据功能关系可知，线框的重力势能减小转化为动能和电能，则线框中产生的焦耳热小于
+mgh．故C错误，D正确．
故选：ABD
B、线框bc边刚进入磁场时，感应电动势 E=BLv，感应电流 I=
| BLv |
| R |
| B2L2v |
| R |
又 F=mg
解得，线框速度的大小 v=
| mgR |
| B2L2 |
C、D、在线框从开始下落到bc边刚进入磁场的过程中，重力做功W1，根据动能定理得：
W1=
| 1 |
| 2 |
| 1 |
| 2 |
| mgR |
| B2L2 |
| m3g2R2 |
| 2B4L4 |
在线框从bc边刚进入磁场到ad边刚进入磁场的过程中，重力做功W2．
W2=mgh
所以在线框从开始下落到ad边刚进入磁场的过程中，重力做功：W=W1+W2=
| m3g2R2 |
| 2B4L4 |
根据功能关系可知，线框的重力势能减小转化为动能和电能，则线框中产生的焦耳热小于
| m3g2R2 |
| 2B4L4 |
故选：ABD
点评：本题是电磁感应中的力学问题，求解安培力和分析能量如何转化是两个关键，考查电磁感应、动能定理、平衡条件等知识综合应用和分析能力．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，矩形单匝导线框abcd竖直放置，其下方有一磁感应强度为B的有界匀强磁场区域，该区域的上边界PP′水平，并与线框的ab边平行，磁场方向与线框平面垂直．已知线框ab边长为L1，ad边长为L2，线框质量为m，总电阻为R．现无初速地释放线框，在下落过程中线框所在平面始终与磁场垂直，且线框的ab边始终与PP′平行．重力加速度为g．若线框恰好匀速进入磁场，求：
