题目内容
海豚靠尾部来推动下部的水,能够从水中高高跃起,被誉为“会飞的鱼”.一身长l=1.8m,质量m=65kg的海豚,跃起后从h1=1.0m的高度处自由下落,尾部接触水面后经过时间t=0.25s身体速度降为零,紧接着尾部用力F向下拍打水,又向上跃起h2=0.5m,假定上升、下降两个阶段尾部与水的作用力分别都是恒力,求上升阶段尾部与水的作用力F.(取g=10m/s2)
解:自由下落1.0m的末速度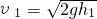 =
= .
.
在减速时间为0.25s的匀减速阶段,重心下落的高度 =0.56m.
=0.56m.
竖直向上跃起的速度
离开水面之前上升的加速度:
设尾部与水面的作用力F,由牛顿第二定律有:F-mg=ma
解得F=m(g+a)=1230N.
答:上升阶段尾部与水的作用力F=1230N.
分析:先分析海豚跃起后从h1=1.0m的高度处下落过程,先自由下落,后进入水中做匀减速运动,根据速度位移公式求出海豚落水时的速度,再用平均速度公式求出海豚在水中重心下降的高度.再研究海豚上升的过程,根据速度位移公式求出离开水面之前上升的加速度,由牛顿第二定律求出上升阶段尾部与水的作用力F.
点评:本题一要建立模型,简化过程;二要抓住下降与上升两个过程之间的联系.
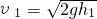 =
= .
.在减速时间为0.25s的匀减速阶段,重心下落的高度
 =0.56m.
=0.56m.竖直向上跃起的速度

离开水面之前上升的加速度:

设尾部与水面的作用力F,由牛顿第二定律有:F-mg=ma
解得F=m(g+a)=1230N.
答:上升阶段尾部与水的作用力F=1230N.
分析:先分析海豚跃起后从h1=1.0m的高度处下落过程,先自由下落,后进入水中做匀减速运动,根据速度位移公式求出海豚落水时的速度,再用平均速度公式求出海豚在水中重心下降的高度.再研究海豚上升的过程,根据速度位移公式求出离开水面之前上升的加速度,由牛顿第二定律求出上升阶段尾部与水的作用力F.
点评:本题一要建立模型,简化过程;二要抓住下降与上升两个过程之间的联系.

练习册系列答案
相关题目