题目内容
16. 如图所示将重为G的物体A放在倾角为37°的斜面上,A与斜面间的摩擦因数为0.1,那么对A施加一个可能多大的水平力,可使A物体保持静止状态?(设A物体受到的最大静摩擦力与滑动摩擦力大小相等,sin37°=0.6 cos37°=0.8)
如图所示将重为G的物体A放在倾角为37°的斜面上,A与斜面间的摩擦因数为0.1,那么对A施加一个可能多大的水平力,可使A物体保持静止状态?(设A物体受到的最大静摩擦力与滑动摩擦力大小相等,sin37°=0.6 cos37°=0.8)
分析 本题考虑恰好不上滑和恰好不下滑两种临界情况,对物体受力分析,根据正交分解法,运用共点力平衡求出水平力F大小的范围.
解答 解:当物体A有沿着斜面向上运动的趋势时,其受力如图甲所示.
沿着斜面、垂直斜面建立坐标系,由平衡条件得:
在x轴上:Fcosα-f=Gsinα ①
在y轴上:FN=Gcosα+Fsinα ②
摩擦力:fm=μFN ③
由以上三式解得:F=$\frac{34}{37}$G
当物体A有沿着斜面向下运动的趋势时,其受力如图乙所示.
在x轴上:Fcosα+f=Gsinα ④
在y轴上:FN=Gcosα+Fsinα ⑤
摩擦力:fm=μFN ⑥
由④⑤⑥得作用力:F=$\frac{26}{43}$G
综上,水平力F的取值范围为:$\frac{26}{43}$G≤F≤$\frac{34}{37}$G.
答:对A施加一个水平力在范围:0.45G≤F≤0.72G,可使A物体保持静止状态.
点评 解决本题的关键正确地进行受力分析,抓住合力等于零,找到临界条件,运用正交分解进行求解;注意物体可静摩擦力可以平行斜面向上,也可能平行斜面向下.

练习册系列答案
相关题目
6.某兴趣小组设计了一个滚筒式炒栗子机器,滚筒内表面粗糙,内直径为D.工作时滚筒绕固定的水平中心轴转动.为使栗子受热均匀,要求栗子到达滚筒最高处前与筒壁脱离,则( )
| A. | 滚筒的角速度应满足ω<$\sqrt{\frac{2g}{D}}$ | |
| B. | 滚筒的角速度应满足ω>$\sqrt{\frac{2g}{D}}$ | |
| C. | 栗子脱离滚筒的位置与其质量有关 | |
| D. | 若栗子到达最高点时脱离滚筒,栗子将自由下落 |
7. 如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( )
如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( )
 如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( )
如图所示,质量为m的小球用长为L的细绳与O点相连,开始时小球位于A点,OA长为L,在OA的垂直平分线BC和虚线OD的交点处有一小钉,虚线OD与水平方向的夹角θ=37°,当小球由静止释放,小球运动到最低点时,细绳刚好断开(不考虑细绳与小钉碰撞的能量损失),则绳能承受的最大拉力为( )| A. | 2mg | B. | 3mg | C. | 4mg | D. | 5mg |
4. 如图所示为水平向右的匀强电场中的一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行,a、b为水平直径两端,c为最高点,d为最低点,一质量为m、带电荷量为+q的质子能沿轨道内侧运动,且通过弧ac的中点c时对轨道无作用力,通过b点时对轨道压力为Fb,取d点的电势φd=0,重力加速度为g.则( )
如图所示为水平向右的匀强电场中的一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行,a、b为水平直径两端,c为最高点,d为最低点,一质量为m、带电荷量为+q的质子能沿轨道内侧运动,且通过弧ac的中点c时对轨道无作用力,通过b点时对轨道压力为Fb,取d点的电势φd=0,重力加速度为g.则( )
 如图所示为水平向右的匀强电场中的一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行,a、b为水平直径两端,c为最高点,d为最低点,一质量为m、带电荷量为+q的质子能沿轨道内侧运动,且通过弧ac的中点c时对轨道无作用力,通过b点时对轨道压力为Fb,取d点的电势φd=0,重力加速度为g.则( )
如图所示为水平向右的匀强电场中的一半径为r的光滑绝缘圆轨道,轨道平面与电场方向平行,a、b为水平直径两端,c为最高点,d为最低点,一质量为m、带电荷量为+q的质子能沿轨道内侧运动,且通过弧ac的中点c时对轨道无作用力,通过b点时对轨道压力为Fb,取d点的电势φd=0,重力加速度为g.则( )| A. | 该匀强电场的电场强度大小为E=$\frac{mg}{2q}$ | |
| B. | 质点在b点的电势能为mg | |
| C. | 质点在d点的速率最大 | |
| D. | 质点在a点对轨道的压力大小为Fb-6mg |
11.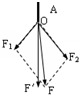 某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结点.实验时以下说法正确的是( )
某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结点.实验时以下说法正确的是( )
 某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结点.实验时以下说法正确的是( )
某同学做《共点的两个力的合成》实验作出如图所示的图,其中A为固定橡皮条的固定点,O为橡皮条与细绳的结点.实验时以下说法正确的是( )| A. | F1、F2的大小以及F1、F2间的夹角应当尽可能大些 | |
| B. | 图中F1、F2合力的理论值和实验值中,一定与AO共线的是F | |
| C. | 单独拉一个绳套和同时拉两个绳套时,只要保证橡皮条的伸长量相同即可 | |
| D. | 绳套的长度应当适当长些 |
5.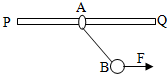 如图所示,水平固定杆PQ上套有一轻质细环A,环A和球B间用一轻质绳相连,球B的质量为m,环A与杆间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,现用水平向右的外力F=$\frac{{\sqrt{3}}}{2}$mg作用在球B上,系统稳定时,A、B一起运动的加速度为( )
如图所示,水平固定杆PQ上套有一轻质细环A,环A和球B间用一轻质绳相连,球B的质量为m,环A与杆间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,现用水平向右的外力F=$\frac{{\sqrt{3}}}{2}$mg作用在球B上,系统稳定时,A、B一起运动的加速度为( )
 如图所示,水平固定杆PQ上套有一轻质细环A,环A和球B间用一轻质绳相连,球B的质量为m,环A与杆间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,现用水平向右的外力F=$\frac{{\sqrt{3}}}{2}$mg作用在球B上,系统稳定时,A、B一起运动的加速度为( )
如图所示,水平固定杆PQ上套有一轻质细环A,环A和球B间用一轻质绳相连,球B的质量为m,环A与杆间的动摩擦因数为μ=$\frac{{\sqrt{3}}}{3}$,现用水平向右的外力F=$\frac{{\sqrt{3}}}{2}$mg作用在球B上,系统稳定时,A、B一起运动的加速度为( )| A. | $\frac{{\sqrt{3}}}{6}g$ | B. | $\frac{{\sqrt{3}}}{4}g$ | C. | $\frac{{\sqrt{3}}}{3}g$ | D. | $\frac{{\sqrt{3}}}{2}g$ |
6.某同学探究弹力与弹簧伸长量的关系,将弹簧悬挂在铁架上,刻度尺固定在弹簧一侧,弹簧轴线和刻度尺都在竖直方向上,在弹簧下端依次增加相同规格钩码的个数,数据记录如表:
(1)在数据记录表中,有一个记录不规范的数据是14.2;根据记录的数据可知,所用刻度尺的分度值是1mm.
(2)请在如图所示的坐标图中画出弹簧的伸长量△L与所挂钩码个数N的关系图象.
(3)根据图象可知,当挂6个钩码时,弹簧的伸长量3.28cm(未超过弹簧的弹性限度).

| 所挂钩码数量N(个) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 弹簧长度L(cm) | 12.56 | 13.11 | 13.65 | 14.2 | 14.73 | 15.29 | |
| 伸长量△L(cm) | 0 | 0.55 | 1.09 | 1.64 | 2.17 | 2.73 |
(2)请在如图所示的坐标图中画出弹簧的伸长量△L与所挂钩码个数N的关系图象.
(3)根据图象可知,当挂6个钩码时,弹簧的伸长量3.28cm(未超过弹簧的弹性限度).

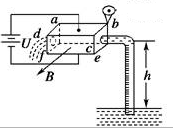 如图所示是一种电磁泵,泵体是一个长方体,端面是一个边长为σ的正方形,ab长为l,上下两面接在电源上,电压为U(内阻不计).磁感应强度为B的磁场指向cdfe面,液体电阻率为ρ,密度为D(液体原来不导电,在泵头通入导电剂后才导电)
如图所示是一种电磁泵,泵体是一个长方体,端面是一个边长为σ的正方形,ab长为l,上下两面接在电源上,电压为U(内阻不计).磁感应强度为B的磁场指向cdfe面,液体电阻率为ρ,密度为D(液体原来不导电,在泵头通入导电剂后才导电) 有一个直径为L=1.5m的圆形桌子,桌面离地高度为h=1.25m.一个小物块从桌面正中心O点以初速v0=2m/s沿着桌面做直线运动最后落在水平地面上.已知动摩擦因数为μ=0.2,取g=10m/s2,求:
有一个直径为L=1.5m的圆形桌子,桌面离地高度为h=1.25m.一个小物块从桌面正中心O点以初速v0=2m/s沿着桌面做直线运动最后落在水平地面上.已知动摩擦因数为μ=0.2,取g=10m/s2,求: