题目内容
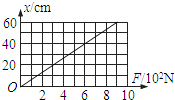
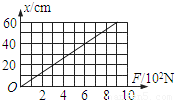
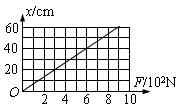
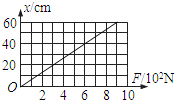 一根轻弹簧的伸长跟所受的外力(F)之间的关系如图所示,试求:
一根轻弹簧的伸长跟所受的外力(F)之间的关系如图所示,试求:(1)弹簧的劲度系数k;
(2)若弹簧原长l0=60cm,当把弹簧压缩到40cm长时,需要多大的压力F?
(3)如果用600N的拉力(仍在弹性限度内,弹簧原长同上),弹簧长度l是多少?
分析:胡克的弹性定律是指:弹簧在发生弹性形变时,弹簧的弹力F和弹簧的伸长量(或压缩量)x成正比,即F=k?x.k是弹簧的劲度系数,它由材料的性质所决定.
解答:解:(1)从图象可以看出弹簧的形变量与弹簧受到的力成正比,
由胡克定律F=kx,
整理得:x=
F
由公式可看出图象的斜率等于劲度系数的倒数,
所以弹簧的劲度系数:k=1500N/m,
(2)若弹簧原长l0=60cm,当把弹簧压缩到40cm长,
此时弹簧的压缩量:x=20cm
由胡克定律F=kx,
解得:F=300N
(3)如果用600N的拉力,
由胡克定律F=kx,
解得:弹簧被拉长△l=40cm
所以弹簧的总长度为:l=l0+△l=100cm
答:(1)弹簧的劲度系数为1500N/m.
(2)当把弹簧压缩到40cm长时,需要300N的压力.
(3)弹簧长度 l=100cm.
由胡克定律F=kx,
整理得:x=
| 1 |
| k |
由公式可看出图象的斜率等于劲度系数的倒数,
所以弹簧的劲度系数:k=1500N/m,
(2)若弹簧原长l0=60cm,当把弹簧压缩到40cm长,
此时弹簧的压缩量:x=20cm
由胡克定律F=kx,
解得:F=300N
(3)如果用600N的拉力,
由胡克定律F=kx,
解得:弹簧被拉长△l=40cm
所以弹簧的总长度为:l=l0+△l=100cm
答:(1)弹簧的劲度系数为1500N/m.
(2)当把弹簧压缩到40cm长时,需要300N的压力.
(3)弹簧长度 l=100cm.
点评:理解胡克定律的关键点是:形变量x既可以是伸长量,也可以是压缩量.

练习册系列答案
相关题目
 一根轻弹簧的伸长跟所受的外力(F)之间的关系如图所示,试求:
一根轻弹簧的伸长跟所受的外力(F)之间的关系如图所示,试求: