题目内容
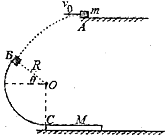
【题目】在光滑水平桌面中央固定一边长为0.3 m的正三棱柱abc，俯视如图所示。长度为L=1 m的细线，一端固定在a点，另一端拴住一质量为m=0.5 kg、不计大小的小球。初始时刻，把细线拉直在ca的延长线上，并给小球以v0=2 m/s且垂直于细线方向的水平速度，由于棱柱的存在，细线逐渐缠绕在棱柱上（不计细线与三棱柱碰撞过程中的能量损失）。已知细线所能承受的最大拉力为7 N，则下列说法中不正确的是
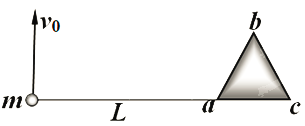
A. 细线断裂之前，小球速度的大小保持不变
B. 细线断裂之前，小球所受细线拉力的冲量为零
C. 细线断裂之前，小球运动的总时间为0.7π s
D. 细线断裂之前，小球运动的位移大小为0.1 m
【答案】D
【解析】细线断裂之前，绳子拉力与速度垂直，不做功，不改变小球的速度大小，故小球的速度大小保持不变．故A正确．细线断裂之前，小球所受细线拉力不为零，故拉力的冲量不为零，选项B错误；绳子刚断裂时，拉力大小为7N，由
得，此时的半径为
，由于小球每转120°半径减小0.3m，则知小球刚好转过一周，细线断裂，则小球运动的总时间为： 
，而r1=1m，r2=0.7m，r3=0.4m，v0=2m/s，解得：t=0.7π s．故C正确．小球每转120°半径减小0.3m，细线断裂之前，小球运动的位移大小为1m-0.1m=0.9m．故D错误．故选AC．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
【题目】为了节能和环保，一些公共场所使用光控开关控制照明系统．光控开关可采用光敏电阻来控制，光敏电阻是阻值随着光的照度而发生变化的元件（照度可以反映光的强弱，光越强照度越大，照度单位为lx）．某光敏电阻RP在不同照度下的阻值如下表：
照度（lx） | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 |
电阻（kΩ） | 75 | 40 | 28 | 23 | 20 | 18 |
（1）根据表中数据，请在给定的坐标系中描绘出阻值随照度变化的曲线.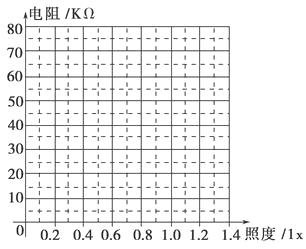
（2）由图线可知阻值随照度变化的特点是： ．
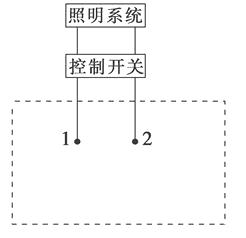
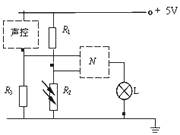
（3）如图所示，当1、2两端所加电压上升至2 V时，控制开关自动启动照明系统．请利用下列器材设计一个简单电路，给1、2两端提供电压，要求当天色渐暗照度降低至1.0（lx）时启动照明系统。
光敏电阻RP（符号 
，阻值见上表）；
提供的器材如下：直流电源E（电动势3 V ， 内阻不计）；
定值电阻：R1＝10 kΩ，R2＝20 kΩ，R3＝40 kΩ；
开关S及导线若干．图中定值电阻应该选择： ．
（4）请在虚线框内完成电路原理图．（不考虑控制开关对所设计电路的影响）
